Продолжение - решение
Cтраница 4
Следует отметить, что применение метода продолжения решения непосредственно к уравнениям краевой задачи не связывает его численную реализацию с каким-либо конкретным способом алгебраизации исходной задачи и открывает возможности использования самых различных методов для решения пошаговых линейных краевых задач. [46]
Рассмотренный здесь подход приводит к задаче продолжения решения ty ( x, у) уравнения ( 0.1.1 а), регулярного в области 2), на комплексные значения х и у. [47]
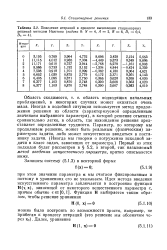 |
Поведение итераций в процессе вычисления стационарных решений методом Ньютона ( задача 8. N 4, А 2, В 6, Л, 0 4. [48] |
Иногда в подобной ситуации используется метод продолжения решения из области ( характеризуемой определенным значением выбранного параметра), в которой решение отыскать сравнительно легко, в область, где нахождение решения представляет определенные трудности. Параметр, по которому мы продолжаем решение, может быть реальным ( физическим) параметром задачи, либо может искусственно вводиться в постановку задачи. Иногда мы говорим о погружении исходной задачи в класс задач, зависящих от параметра. Первый из этих подходов будет рассмотрен в § 5.2, а второй, так называемый метод введения искусственного параметра, кратко описывается ниже. [49]
Наиболее целесообразен в зтом случае метод продолжения решения. В основу метода положено дифференциальное уравнение (10.43) колебаний прямолинейного стержня. [51]
На таком многообразии неверна теорема единственности продолжения решений дифференциального уравнения, хотя локальная теорема единственности и верна. [52]
Большое число исследований связано с применением метода продолжения решения к классической нелинейной задаче конечных и больших прогибов оболочек вращения. [53]
Страницы: 1 2 3 4
