Периодическое продолжение

Cтраница 1

Периодическое продолжение ф с периодом 2Я 2 изображено на рис. 2 в гл. [1]

Кроме того, при периодическом продолжении она остается непрерывной. [2]

За его пределами следует брать периодические продолжения этих функций. [3]

Теорема I не утверждает, что только периодическое продолжение периодического решения Т ( t на начальное множество определяет это решение. [4]

Гргфик f ( t) и ее периодическое продолжение ер ( t) ( так называемая пилообразная функция) представлены на рис. 2.6, а, откуда видно, что f ( t) на [ О, Т ] удовлетворяет условиям Дирихле. [5]

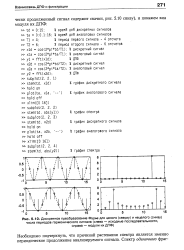Дискретное преобразование Фурье для целого ( сверху и нецелого ( снизу числа периодов гармонического сигнала ( слева - исходные последовательности. [6]

Необходимо подчеркнуть, что причиной растекания спектра является именно периодическое продолжение анализируемого сигнала. [7]

В) ( о Г ( Х) - периодических продолжениях решения Ф ( t)) не имеет решений. [8]

Если характеристическая функция равна нулю при t а, то все ее периодические продолжения с периодом 2Я, 2а тоже являются характеристическими функциями. [9]

Вне интервала [ 0 1) ряд (14.38), как отмечалось в § 14.4, описывает периодическое продолжение s1 ( 0), в данном примере гармоническую функцию. [10]

Верно ли обратное утверждение: если для коэффициентов Фурье верна последняя оценка, то функция допускает голоморфное периодическое продолжение в указанную полосу. [11]

Аналогично, так как все члены ряда ( 103) - четные функции, то его сумма дает четное периодическое продолжение функции f ( x) с интервала О лг л на всю ось с периодом 2л; сумма же ряда ( 104) дает нечетное продолжение с тем же периодом. [12]

Пусть x ( t) представляет собой такой действительный сигнал длительностью L с, что ряд Фурье его периодического продолжения не содержит гармоник с номером выше А. [13]

После соответствующего изменения g около точки а и а 2я мы получаем новую функцию g, которая после периодического продолжения все же принадлежит B ( fe, и новую функцию h f - - g, удовлетворяющую требуемым условиям. [14]

В дальнейшем, если это не оговорено, будем изучать только такие периодические решения, определяемые начальными вектор-функциями, которые являются периодическим продолжением периодического решения на начальное множество. [15]

Страницы: 1 2 3