Производная - вектор
Cтраница 1
Производная вектора по скаляру представляет собой также вектор. [1]
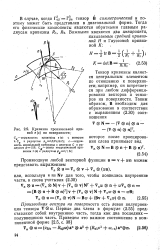 |
Кривизна произвольной кривой r ( s на поверхности. ]. [2] |
Производная вектора на поверхности есть левая полупроек. Первые два члена в формуле (2.55) представляют собой внутреннюю часть, тогда как два последних-г полувнешнюю часть. [3]
Производная вектора N в (70.1) берется относительно инерциаль-ной ( неподвижной) системы координат. [4]
Производная вектора угловой скорости по времени - - е называется угловым ускорением. [5]
Производная вектора количества движения р по времени является вектором, следовательно, сила также должна быть вектором. [6]
Производная вектора количества движения системы по времени равна геометрической сумме всех внешних сил, действующих на систему. [7]
Когда производная вектора mv перпендикулярна самому вектору, модуль вектора не меняется, меняется только его направление. [8]
Действительно, производная вектора а по произвольному направлению с может быть определена путем следующего геометрического построения. [9]
Итак, производная вектора с постоянным модулем перпендику - лярна к нему. [10]
Действительно, производная вектора а по произвольному направлению с может быть определена путем следующего геометрического построения. [11]
Действительно, производная вектора а по произвольному направлению с может быть определена путем следующего геометрического построения. [12]
Итак, производная вектора по его скалярному аргументу есть вектор, направленный по касательной к годографу исходного вектора в рассматриваемой точке. [13]
Итак, производная вектора с постоянным модулем перпендикулярна к нему. [14]
Как направлена производная вектора и чему равен ее модуль. [15]
Страницы: 1 2 3