Обобщенный процесс

Cтраница 1

Обобщенный процесс - , где - стандартный процесс с некоррелированными приращениями, называют слабым белым шумом. [1]

Действительный обобщенный процесс Л ( ф) называют процессом с независимыми значениями, если для любых ф - g 3) r, t I, 2, для которых ф О, случайные величины Л ( cpj) и А ( ф2) независимы. [2]

Поэтому обобщенный процесс Винера включает основной процесс Винера наравне с элементом тенденции. Элемент тенденции является детерминированным, т.е. неслучайным, а основной процесс Винера представляет собой стохастический элемент. На рис. 10.3 изображен один из таких процессов, где ясно заметно влияние положительной тенденции. Обобщенный процесс Винера может рассматриваться как непрерывный во времени эквивалент субмартингального процесса. [3]

Гауссовость обобщенного процесса ( и, ) означает, что все случайные величины ( и, I), iff /, имеют гауссовское распределение вероятностей. [4]

Хотя для обобщенного процесса понятие значения процесса в фиксированный момент времени не определено, все же можно дать естественное определение обобщенного процесса с независимыми значениями и показать, что белый шум является таковым. [5]

Из определения гауссовского обобщенного процесса непосредственно вытекает, что его производные любого порядка также являются гауссовскими обобщенными процессами. [6]

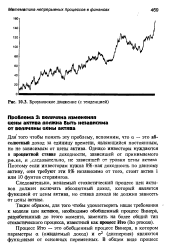Броуновское движение ( с тенденцией. [7]

Процесс Ито - это обобщенный процесс Винера, в котором параметры а ( ожидаемый доход) и ст2 ( дисперсия) являются функциями от основных переменных. [8]

Очевидно, если Л - обобщенный процесс, то все его производные также являются обобщенными случайными процессами. [9]

Формула ( 1) для обобщенного процесса и формула ( 5) для обыкновенного процесса называются спектральным разложением стационарного случайного процесса. [10]

Характеристический функционал однозначно определяет конечномерные распределения обобщенного процесса. [11]

Я ( со) - спектр обобщенного процесса, амплитуды которого увеличены в - - - 2п раз. [12]

Процесс вида ( 4) называется обобщенным процессом Пуассона. [13]

Tt и х и является также обобщенным процессом Пуассона с характеристической функцией как и в процессе КО. [14]

Как известно ( см. [5, 6]), гауссовский стационарный обобщенный процесс ( ф) однозначно характеризуется обобщенной корреляционной функцией йс. [15]

Страницы: 1 2 3