Немарковский процесс

Cтраница 1

Немарковский процесс удовлетворяющий уравнению Колмогорова-Чаплина. Поэтому сначала представлялось интуитивно ясным, что ни один немарковский процесс не должен удовлетворять этому тождеству; это предположение, казалось, подтверждалось тем фактом, что вероятности перехода за п шагов для такого процесса должны удовлетворять целому множеству любопытных тождеств. [1]

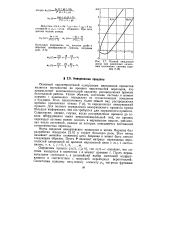Полный ожидаемый доход при различных начальных состояниях системы ( пример. [2]

Метод сведения немарковских процессов к цепям Маркова был разработан Кендалом [2.5] и играет большую роль. Этот метод называют методом вложенной цепи Маркова и может быть описан следующим образом. [3]

Это также означает, что для немарковских процессов представление многомерной плотности вероятности в виде ( G. [4]

Простой метод оценки относительной вероятности в немарковских процессах использован фирмой Абт ассо-шиэйтс в операционных моделях ( см., например, [83]): для каждого из взаимосвязанных классов возможностей подсчитывается число способов достижения того или иного конкретного результата, которое и принимается за меру вероятности; например, результат, который может быть достигнут десятью различными способами, в два раза более вероятен, чем результат, которого можно достигнуть всего лишь пятью способами. [5]

Маркова, и, наконец, привести несколько примеров немарковских процессов. [6]

Заметим, что за счет расширения пространства состояний процесса можно немарковский процесс превратить в марковский. Одна из возможностей такого рода преобразования состоит в следующем. [7]

Стоит отметить, однако, что могут существовать ( довольно патологические) немарковские процессы с теми же переходными вероятностями. Этот вопрос подробно обсуждался в разд. [8]

Полезность потоков Эрланга состоит в том, что с их помощью можно сводить немарковские процессы к марковским. [9]

Близкие по существу рассуждения позволяют проверить условия F и Fx и для некоторых немарковских процессов с хорошими свойствами перемешивания ( ср. [10]

Ниже будет приведен ряд примеров, общее назначение которых - показать, каким образом немарковский процесс превратить в марковский, расширив множество состояний. [11]

Потоки Эрланга в классе потоков Пальма обладают тем преимуществом, что с их помощью можно сводить немарковские процессы к марковским. [12]

Описанный выше процесс ( /) ( при нефиксированной реализации ( x ( t)) является немарковским процессом. [13]

Основное преимущество рассматриваемого подхода состоит в том, что мы получаем возможность использовать теорию цепей Маркова для получения некоторой информации о немарковском процессе. [14]

Псевдосостояние U может иметь самую различную структуру, однако структура, изображенная на рис. 5.3.1, является достаточно простой для проведения различного моделирования немарковских процессов. [15]

Страницы: 1 2 3