Итерационный процесс
Cтраница 1
Итерационный процесс с указанным оптимальным набором параметров называется чебышевским. [1]
Итерационный процесс сходится, но приближения колеблются около точного значения корня. [2]
Итерационный процесс при этом в общем случае расходится. [3]
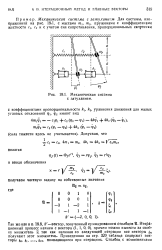 |
Механическая система с затуханием. [4] |
Итерационный процесс начнем с вектора ( 1, 1, 0, 0), причем можно вынести за скобку множитель 2, так как начиная со следующей итерации все векторы jv получают этот множитель. [5]
Итерационный процесс (6.1.13) сходится в W l) ( П), начиная С произвольного начального гладкого приближения. Теоретически этот процесс можно применить для расчета любых магнитных систем. [6]
Итерационный процесс может быть организован несколько иначе. Этот подход описан ниже при построении решения задачи Римана для стационарных уравнений мелкой воды ( разд. В этом случае ( рп является более гладкой функцией, в частности, непрерывной при / 3 рп и р рп. [7]
Итерационный процесс не всегда приводит к сошедшемуся решению. Иногда значения ф колеблются от итерации к итерации или все время плывут. Такой расходимости итерационного процесса следует избегать. [8]
Итерационный процесс должен быть построен так, чтобы последовательные приближения х ( р) с ростом номера р стремились к решению х уравнения. [9]
Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его величина достигнет некоторого заданного малого числа е, итерации прекращаются и происходит вывод результатов. [10]
Итерационный процесс для определения узловых точек zk, изложенный в § 59 так подробно только из методических соображений, можно значительно упростить. [11]
Итерационный процесс выполняем при помощи шаблонов приложения II, которые надо разрезать на отдельные карточки, в соответствии с их номерами. [12]
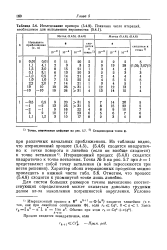 |
Исследование примера. Показано число итераций, необходимое для выполнения неравенства. [13] |
Итерационный процесс (5.4.8) сходится квадратично к точке ветвления. Характер обоих итерационных процессов можно проследить в нижней части табл. 5.6. Отметим, что процесс (5.4.8) сходится к упомянутой точке лишь линейно. [14]
Итерационный процесс прекращается, когда разница между двумя последовательными приближениями оказывается меньше заданной точности. [15]
Страницы: 1 2 3 4