Путь - нагружение
Cтраница 2
Уравнения (16.5.4) представляют собою параметрические уравнения предельного пути нагружения, выходящего из точки Q, для которого соотношения деформационной теории пластичности (16.5.3) еще остаются справедливыми. Заменив р на - р, мы получим симметричную кривую, соответствующую тому случаю, когда точка А остается на месте, а движется точка В. [16]
Отметим, что при развитом течении, путь нагружения которого стремится к некоторой прямой, точки Д, Oi, 0 % будут стремиться занять положение на одной прямой. [17]
Мы видим, что предыдущая группа соотношений определяет путь нагружения, соответствующий данному пути деформирования. [18]
Постулат пластичности справедлив для более широкого класса материалов и путей нагружения, чем постулат Друккера [128], являющийся лишь достаточным, но не необходимым условием для выполнения постулата пластичности. [19]
Переходы третьего порядка обычно наблюдаются в функциях отклика при путях нагружения с неравными главными напряжениями. [21]
Несмотря на эффекты нелинейности и весьма сложную ситуацию при путях нагружения общего вида, в теориях пластических тел с угловой точкой на 2Р возникают значительные упрощения для некоторого множества путей нагружения, полностью принадлежащих области полного нагружения. В частности, Будянским), было показано, что для некоторой совокупности путей полного нагружения можно рассматривать конечные соотношения между напряжениями и деформациями. Рассмотренные выше общие идеи построения моделей пластических тел были развиты в основном в последние полтора десятилетия. Экспериментальные исследования введенных функций пока немногочисленны. [22]
Рассмотрим применение вышеизложенной теории к определению пластических деформаций при лучевых путях немонотонного нагружения. [23]
Третий вариант пути нагружения, Рассмотрены три вида этого варианта пути нагружения. [24]
Анализ экспериментальных исследований закономерностей повторного и циклического деформирования [8-14] при лучевых путях нагружения ( растяжение-сжатие, знакопеременное нагру-жение) позволяет сделать следующие выводы. [25]
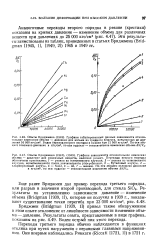
На рис. 1 и 2 приведены схемы использованных для опытов вариантов пути нагружения ( / - VI) в той последовательности, в которой были проведены опыты. [26]
Однако небольшое размышление убеждает нас в том, что при рассмотрении путей нагружения составляющие движения точки Р ( 0ь 02, 03), направленные вверх или вниз вдоль оси цилиндра, несущественны, поскольку присутствие этих составляющих означает прибавление или вычитание из. [27]
Эти напряжения создают деформационную анизотропию материала, которая проявляется при изменении направления пути нагружения. [28]
Вопрос, является ли указанная диаграмма единой для различных напряженных состояний и путей нагружения, интересен и в следующем отношении. В некоторых работах зависимость размера зерна от предшествовавшей отжигу пластической деформации использована для экспериментального определения величины этой деформации. При этом диаграмма рекристаллизации растянутого материала использована в качестве градуи-ровочного графика. Для того чтобы такое определение деформации было обоснованным, необходимо убедиться в универсальности указанной диаграммы. [29]
Было показано, что соотношения деформационной теории Генки-Надаи могут иметь место для путей нагружения, отличных от пропорционального. [30]
Страницы: 1 2 3 4