Радиус - кривизна - срединная поверхность
Cтраница 3
В начале пластической деформации краевой части заготовки при значительных углах конусности наблюдается некоторое уменьшение усилия раздачи, объясняемое тем, что при увеличении диаметра краевой части уменьшается усилие по пуансону, необходимое для создания изгибающего момента постоянной величины. Снижению усилия способствует и увеличение радиусов кривизны RQ срединной поверхности в очаге деформации. [31]
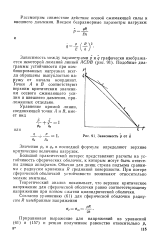 |
Зависимость р от q. [32] |
Большой практический интерес представляют расчеты на устойчивость сферических оболочек, к которым могут быть отнесены днища аппаратов. Обычно для днищ стрела подъема сравнима с радиусом кривизны R срединной поверхности. При потере сферической оболочкой устойчивости возникают относительно мелкие вмятины. [33]
Нелинейный характер распределения компонент тензора напряжений по координате х3, характеризующий напряженное состояние толстостенных оболочек, обусловлен быстрым изменением метрики пространства, занимаемого оболочкой. Отказ от геометрической гипотезы о малости отношения толщины к радиусу кривизны срединной поверхности и учет изменения метрики по координате л3 делают эффективными соотношения (1.84), (1.93) - (1.94), (1.102) - (1.104), (1.114) - (1.116), (1.118) для исследования толстостенных оболочек. [34]
Во многих областях техники применяют сферические оболочки в виде сегментов, закрепленных по краю. Следует различать сегменты с большим углом охвата, стрела подъема Н которых сравнима с радиусом кривизны срединной поверхности R ( рис. 32), и пологие панели, для которых Н R. [35]
Увеличение ширины фланца при неизменном наружном диаметре происходит вследствие изменения внутреннего диаметра фланца путем перехода части поверхности, втянутой в матрицу на предыдущем переходе, во фланцевую часть заготовки на данном переходе вытяжки. Так как часть заготовки, переходящая во фланец на предыдущем переходе, была обтянута по кромке матрицы и имела определенный радиус кривизны срединной поверхности в меридиональном сечении, то при переходе во фланец эта часть заготовки должна получить спрямление. [36]
Разница величины радиальных деформаций на стыке зон пластического и упругого изгиба должна обусловливать появление сдвиговых деформаций. При гибке усилием, как было показано ранее, переход от зоны пластического к зоне упругого изгиба приводит к тому, что радиус кривизны срединной поверхности плавно изменяется по длине заготовки от минимального значения в угловой части до бесконечности. При этом величины сдвиговых деформаций, вызванных переменностью радиальных деформаций по длине заготовки, незначительны и обычно в листовой штамповке не учитываются. [37]
В общем случае ( рис. 8.17) очаг деформации можно разделить на три участка: участок / расположен под плоским торцом пуансона; участок / / расположен на скругленной рабочей кромке пуансона и участок / / / находится в зазоре между пуансоном и матрицей. На границах между участками / и / /, между / / и / / / и между / / / и недеформируемой частью элементы заготовки в процессе деформирования получают резкое изменение радиуса кривизны срединной поверхности в меридиональном сечении. [38]
По аналогичным соображениям на рассматриваемых гранях не может быть и поперечных сил. На грани adeh и bcfg могут действовать лишь моменты, стремящиеся повернуть эти грани вокруг касательных к параллельным кругам, проходящим через центры граней, нормальные силы, направленные вдоль меридиана, и поперечные силы, направленные по радиусам кривизны срединной поверхности в этих центрах. [39]
Основу конструкций емкостей давления составляют оболочки. В данной части приводятся зависимости для тонкостенных оболочек. Как показано в работе ПО ], оболочки могут рассматриваться тонкостенными при б - Q 2R, где R - радиус кривизны срединной поверхности. Многочисленные экспериментальные данные подтверждают, что вдали от закрепленных краев оболочек ( l2 5y RS) с достаточной точностью для расчетов могут использоваться формулы безмоментных теорий. [40]
 |
Схема вытяжки плоской заготовки без прижима. [41] |
Дальнейшее опускание пуансона приводит к возникновению меридиональных растягивающих напряжений, достаточных для перевода фланца заготовки ( части, противостоящей плоскости матрицы) в пластическое состояние. С этого момента начинается втягивание заготовки в матрицу с образованием боковых поверхностей вытягиваемого стакана при одновременном уменьшении диаметра заготовки. Однако изгибающий момент в части заготовки, прилегающей к скругленной кромке матрицы, продолжает действовать, так как переход элементов фланца на скругленную кромку матрицы должен сопровождаться значительным изменением радиуса кривизны срединной поверхности этих элементов. [42]
Известно также, что для каждого металла и для каждой схемы напряженного состояния имеется своя допустимая величина деформации, выше которой начинается разрушение. Известно и то, что чем больше влияние растягивающих напряжений на процесс деформации, тем меньше величина допустимой деформации. Следовательно, при изгибе можно ожидать, что разрушение начнется на наружной поверхности заготовки, где растягивающие напряжения оказывают наибольшее влияние на процесс деформации ( сжимающее напряжение ор 0), а деформации растяжения максимальны. Величина деформации ее, возникающей в наружном слое, определяется радиусом кривизны срединной поверхности или же радиусом внутренней поверхности заготовки. [43]
Учитывая, кроме того, симметричность нагрузки вокруг оси, можно заключить, что на грани abed и efgh действуют одинаковые и обратно направленные нормальные силы и моменты, стремящиеся повернуть грань вокруг касательной к срединному меридиану этих граней. Моментов, лежащих в плоскости этих граней и стремящихся повернуть грани вокруг их центров, не существует, так как если бы такие моменты существовали, они имели бы обратные направления на обеих гранях и стремились бы скручивать выделенный элемент, что по соображениям симметрии невозможно. По аналогичным соображениям на рассматриваемых гранях не может быть и поперечных сил. На грани adeh и bcfg могут действовать лишь моменты, стремящиеся повернуть эти грани вокруг касательных к параллельным кругам, проходящим через центры граней, нормальные силы, направленные вдоль меридиана, и поперечные силы, направленные по радиусам кривизны срединной поверхности в этих центрах. [44]
Страницы: 1 2 3