Радиус - пузырь
Cтраница 1
Радиус пузыря находится из решения гидродинамической задачи расширения паровой сферы в несжимаемой жидкости внутри капли. [1]
Радиус пузыря равен г, поверхностное натяжение мыльной пленки а. [2]
Если радиус пузыря увеличивается на dRo, то поглощается тепло dQ LpflwRldRQ, представляющее собой распределенный по сферической поверхности отрицательный источник тепла. Теплота испарения настолько велика, что только она оказывает влияние на последующее распределение температуры. [3]
Если радиус пузырей больше резонансного, то колебания происходят со сдвигом по фазе, наблюдается дисперсия звука, групповая и фазовая скорости различаются и фазовая скорость возрастает. [4]
Нормализованная траектория радиуса пузыря не зависит от распределения температуры в перегретой жидкости, окружающей пузырь. Эта независимость только кажущаяся, поскольку отношение асимметрии, характеризующее величину радиуса пузыря в нормированном виде, зависит от величины отношения времени замедленного роста к длительности всей жизни пузыря. А оба этих параметра, как это видно из уравнения ( 23), требуют знания начального распределения температуры в жидкости. Но эта трудность, как уже отмечалось, не столь уже велика, так как для решения задачи требуется лишь приблизительное представление о начальном распределении температуры. [5]
Здесь г. - радиус пузырей; 1 / ь - скорость пузырей; ms - некоторая постоянная, значение которой будет определено позднее. Сумма бесконечного ряда, стоящая в правой части соотношения ( 4.8 - 4), может быть вычислена. [6]
 |
Сечение через середину центра парообразования, показывающее основные фазы образования, роста и отрыва парового пузыря. [7] |
Таким образом, чем меньше радиус пузыря, тем выше должно быть давление внутри пузыря, чтобы стал возможен его дальнейший рост от минимального или критического радиуса ( что соответствует условиям на рис. 5.6, б) и чтобы мог эффективно действовать центр парообразования. [8]
По уравнению ( 3) радиус растущего пузыря пропорционален корню квадратному из времени. Из данных таблицы вытекает, что в действительности диаметр пузырей, растущих на твердой поверхности, изменяется скорее пропорционально степени времени с меньшим показателем. [9]
 |
Рост и исчезновение пузырей в воде. [10] |
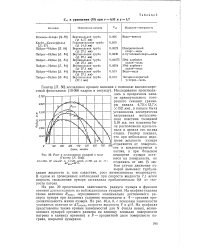
На рис. 39 представлена зависимость радиуса пузыря в функции времени для нескольких из наблюдавшихся пузырей. На графике указана также величина RuaKC, осредненного максимально достижимого радиуса пузыря при заданных условиях теплоотдачи и б - средняя продолжительность жизни пузыря. На рис. 40, а, Ь, с показаны зависимости указанных величин от А7недогр скорости жидкости V и q / A. На графиках представлены также кривые зависимостей для N ( числа новых, возникающих пузырей среднего размера на единицу площади поверхности нагрева в единицу времени) и / - процентной доли поверхности нагрева, покрытой пузырями. [11]
Геометрическое место минимумов не зависит от величины радиуса пузыря а. [12]
Если обозначить через R R ( t) радиус пузыря, пульсирующего в окрестности начала, то скорость его изменения ( которая определяется первым слагаемым) R - тг - кг. [13]
Функция Rf в уравнении ( 21) характеризует радиус изотермического пузыря, давление и температура пара в котором равны давлению и температуре при насыщении на протяжении и стадии роста, и стадии разрушения. [14]
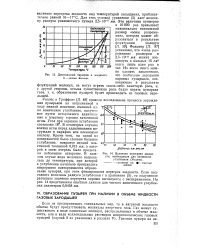 |
Величина перегрева жидкости, необходимая для активации углубления ( Уоллие. [15] |
Страницы: 1 2 3 4