Радиус - пузырь
Cтраница 2
Для этих условий уравнение ( 5) дает величину радиуса равновесного пузыря 2 5 - Ю-3 мм. [16]
Для самого большого из рассматриваемых здесь перегревов ( sslO C) радиус пузыря за это время достигает величины около 0 1 см, что значительно меньше, чем характеристическая длина диффузии. Предположение об однородности температуры внутри паровой области становится по мере уменьшения степени перегрева все более правильным. [17]
Оставшиеся граничные условия выставляются на поверхности пузыря при г. гь, где гь - радиус пузыря. [18]
Мы вычислили по уравнениям ( 1), ( 3) и ( 27) радиус пузыря, скорость и ускорение при движении поверхности раздела пар - жидкость в нормированном виде, а также температуру и давление пара для отношения асимметрии tm / tc / 2 - Результаты этих вычислений отображены на фиг. [19]
Последние два уравнения системы ( 9) показывают, что в рассматриваемом приближении амплитуды колебаний радиуса пузыря с частотой его свободных колебаний затухают. [20]
Приводятся расчеты условий динамического равновесия пузырей пара и воздуха в перегретой воде, показывающие, что радиусы пузырей, находящихся в неустойчивом равновесии, ограничиваются определенной областью значений, которые зависят от температуры воды и начального содержания воздуха в пузыре. Рассматриваются два аналитических решения задачи о скорости роста этих пузырей, находящихся в неустойчивом равновесии: а) решение уравнения роста радиуса пузыря в предположении, что диффузия тепла через стенки пузыря отсутствует; б) решение с учетом диффузии тепла через его стенки. Эти решения сильно отличаются друг от друга. Сопоставление обоих решений с результатами экспериментального исследования скорости роста пузырей в перегретой воде показывает, что второе решение, учитывающее диффузию тепла через стенки пузыря, ближе совпадает с результатами экспериментального исследования. [21]
 |
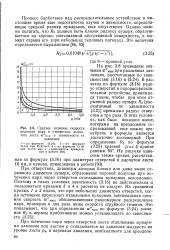
Средние значения гу мжн для водяного пара в зависимости от давления. [22] |
В расчетах по формуле (11.26) диаметр отверстий в парораспределительном устройстве принимался таким, чтобы при этом отрывной радиус пузыря Ro, рассчитанный по зависимости (11.13), превышал радиус отверстия в 3 раза. В этих условиях потерями на преодоление сопротивлений можно пренебречь и формула является достаточно достоверной. [23]
 |
Среднее значение скорости водяного пара в отверстиях дырчатого листа ш Ыин в зависимости от давления. [24] |
В расчетах по формуле (3.16) радиус отверстий в парораспределительном устройстве принимался таким, чтобы при этом отрывной радиус пузыря Ru [ рассчитанный по зависимости (3.2) ] превышал радиус отверстия в три раза. В этих условиях, как было показано выше, потерями на преодоление сопротивлений еще можно пренебречь и формула является достаточно достоверной. [25]
Очевидно, что заданным жидкости внешнему давлению РЖ и температуре жидкости будет соответствовать только одно значение радиуса пузыря ( зародыша), находящегося в метастабильном равновесии с. Однако это равновесие не является устойчивым по отношению к радиусу пузыря; при незначительном уменьшении радиуса пузырь исчезнет; наоборот, при незначительном же его увеличении начнется прогрессирующий рост пузыря. Это значение радиуса, соответствующее метастабильному состоянию, называется критическим; обозначим его через ро. [26]
Для того чтобы получить последние два соотношения, нужно использовать тот факт, что при сделанных предположениях радиусы пузыря и области замкнутой циркуляции газа, связанной с пузырем, практически совпадают. [27]
Задача о диффузии тепла решается в предположении, что толщина пограничного теплового слоя очень мала по сравнению с радиусом пузыря. [28]
При использовании этого уравнения часто е учитывают того, что оно действительно только тогда, когда-диаметр отверстия небольшой и радиус пузыря R0 при отрыве больше радиуса RI. При больших JRi уравнение (11.13) недействительно. Рассчитанный по этой зависимости радиус пузыря 0 оказывается меньше радиуса отверстия RI, что не может соответствовать действительности. Так, в соответствии с уравнением (11.13) при, барботаже пара через воду при давлении 0 1 МПа и температуре воды 373 К отрывной диаметр пузыря превышает диаметр отверстия только тогда, когда R примерно не выше 3 мм. При более высоких давлениях размер радиуса отверстия, при котором уравнение - (11.13) остается справедливым, еще ниже. [29]
При использовании этого уравнения часто не учитывают того, что оно может применяться только тогда, когда диаметр отверстия небольшой и радиус пузыря R0 при отрыве больше радиуса Rt. Рассчитанный по этой зависимости радиус пузыря R0 оказывается меньше радиуса отверстия Rlt что не может соответствовать действительности. Так, в соответствии с (13.11) при барботаже пара через воду для давления 0 1 МПа и температуры воды 100 С отрывной диаметр пузыря превышает диаметр отверстия только тогда, когда jRi 3 мм. При более высоких давлениях размер радиуса отверстия, при котором (13.11) остается справедливой, еще ниже. [30]
Страницы: 1 2 3 4