Величина - математическое ожидание
Cтраница 1
Величина математического ожидания ( LAMBDA) задается на входе. [1]
Величина математического ожидания ( ТНЕТА) задается на входе. Для вычисления натуральных логарифмов на цифровых вычислительных машинах необходимо использовать какие-либо методы аппроксимации, например разложение в степенной ряд. Поэтому, несмотря на легкость программирования, метод обратного преобразования все же работает медленно. [2]
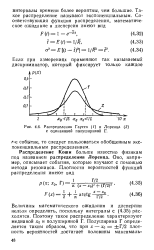 |
Распределения Гаусса ( / и Лоренца ( 2 с одинаковой полушириной Г. [3] |
Величины математического ожидания и дисперсии нельзя определить, поскольку интегралы с (4.35) расходятся. [4]
Величины математического ожидания ЕХ) и среднеквадратиче-ского отклонения ( STD) здесь являются частью исходных данных цикла. [5]
 |
Обобщенная схема регулирования качества линейного строительства магистральных трубопроводов. [6] |
Величина математического ожидания погрешности ( отклонения) отдельного звена размерной цепи характеризует, как правило, систематическую ( динамическую) ошибку системы активного контроля. Однако в реальных ( трассовых) условиях протекания технологических процессов линейного строительства и связанного с ними автоматизированного активного контроля качества может иметь место множество случайных воздействий ( помех), на входе такой системы, что неизбежно будет приводить ее в нестационарный режим функционирования. [7]
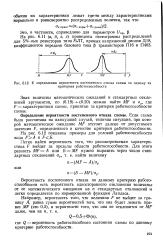 |
К определению вероятности постепенного отказа схемы по одному из критериев работоспособности. [8] |
Зная величины математических ожиданий и стандартных отклонений аргументов, по (6.18) н - (6.20) можно найти MF и ах, где F - характеристики схемы, принятые за критерии работоспособности схемы. [9]
Расчет величины математического ожидания М ( г /) при N 1 и gi I g2 15 - - - 5й 1 - При этом случайные величины Vi, Т / 2, , Vi, входящие в правые части системы дифференциальных уравнений (2.11), заменяются значениями их математических ожиданий. [10]
Следовательно, величину математического ожидания случайной величины можно определить, вычислив ординату центра тяжести плоской фигуры, ограниченной кривой плотности вероятное. [11]
В общем случае величина математического ожидания не выражается в аналитическом виде. Однако легко построить аналитическую верхнюю границу этого ожидания. [12]
Например, В оказывается пропорциональным величине математического ожидания относительного времени простоев оборудования. [13]
 |
Классификация ошибок при запотяении док / мента. [14] |
В работе [144] получены данные о величине математического ожидания ( вероятности) М ( Р) и среднего квадратичного отклонения вероятности D ( Р) появления ошибки ( табл. 7) при заполнении первичных документов на устройствах подготовки информации. [15]
Страницы: 1 2 3 4