Размещение - шар
Cтраница 1
Размещение шаров по ящикам состоит в выборе ящика для каждого шара. [1]
Размещение шаров по ящикам равнозначно выбору ящика для каждого шара. [2]
Простейшее размещение шаров, которое отвечает условию периодического повторения одинаковых слоев, описывается последовательностью АВАВАВ... Ей соответствует упаковка атомов в гексагональной решетке. [3]
Задача о размещении шаров имеет многочисленные приложения. [4]
Предположим, что размещения шаров по ящикам равновозможны. [5]
Условие выбора наугад позволяет считать все размещения шаров равновозможными и использовать модель Лапласа для пт равновероятных исходов. [6]
При шестерной координации наиболее симметричная трехмерная упаковка получается при размещении шаров по точкам примитивной кубической решетки; при этом шарами занято лишь немного более половины пространства. В направлении диагоналей граней или пространственных диагоналей контакты между шарами отсутствуют. [7]
Рассматриваемый опыт можно моделировать с помощью случайного повторного выбора: каждое размещение шара - это случайный выбор с возвращением из номеров ящиков, куда этот шар помещается. Воспользовавшись таким представлением, подсчитаем вероятность того, что заданные / ящиков будут содержать в сумме т шаров. [8]
Получим оценку для ah ( m, п) - числа способов такого размещения шаров no - ячейкам, что точно k ячеек пусты. [9]
I показывает, что самые разнообразные мыслимые эксперименты с абстрактной точки зрения эквивалентны размещению шаров по ящикам. [10]
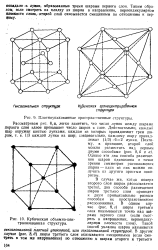 |
Кубическая объемно-централизованная структура. [11] |
В случае же, когда поверх второго слоя шаров располагается третий, два способа размещения шаров третьего слоя приводят к двум принципиально разным способам их пространственного расположения. Такой способ укладки шаров называется гексагональной плотной упаковкой, или гексагональной структурой. [12]
Поэтому существует бесконечное число способов расположения двенадцати шаров, и наиболее симметричное из них - размещение шаров в вершинах правильного икосаэдра - единственного правильного многогранника с 12 вершинами. Длина ребра правильного икосаэдра примерно на 5 % больше расстояния от центра до вершины, так что каждый из 12 шаров внешней оболочки соприкасается только с центральным шаром. И наоборот, для того чтобы каждый из 12 шаров в икосаэдре касался центрального шара и в то же время находился в контакте с пятью соседними шарами, центральный шар должен иметь ра-днус 0 902, если радиус внешних шаров принять за единицу. Икосаэдрическое расположение ближайших соседей вокруг центрального не приводит к периодической трехмерной упаковке шаров, но представляется достаточно интересным для того, чтобы о нем упомянуть. Со структурной точки зрения интересны и некоторые другие упаковки шаров, которые хотя и не дают периодичности в трех измерениях, но так же, как нкосаэдриче-ская, приводят к заполнению всего пространства. [13]
В статистической механике распределение некоторых типов элементарных частиц по ячейкам, на которые разбивается фазовое пространство, соответствует схеме размещения неразличимых шаров. [14]
I, 2, б), мы видим, что очень многие мыслимые эксперименты с абстрактной точки зрения эквивалентны размещению шаров по ящикам. Например, рассматривая грани игральной кости как ящики, получим, что при бросании г раз игральной кости имеется 6Г возможных исходов, в 5Г из которых ни разу не появилась единица. [15]
Страницы: 1 2