Разделенная разность

Cтраница 1

Разделенные разности, введенные в § 1.8, являются ( по доказанному в § 1.8) линейными непрерывными функционалами. [1]

Аналогично разделенные разности могут быть написаны для функций с числом переменных больше двух и представлены на сеточном множестве, более чем двумерном. [2]

Разделенная разность суммы или разности функций равна сумме или разности разделенных разностей слагаемых, соответственно уменьшаемого и вычитаемого. [3]

Конечные и разделенные разности имеют разнообразные применения. В § 9 они используются для построения интерполяционного многочлена. [4]

Если разделенные разности при малом шаге близки к соответствующим производным и во многом им аналогичны, то сами ( неразделенные) разности близки к соответствующим дифференциалам. [5]

Вторые разделенные разности, соответствующие вторым производным, являются разделенными разностями от разделенных разностей. [6]

Таблица разделенных разностей, которая лежит в основе интерполяционной формулы Ньютона, может быть написана в другой, иногда более полезной форме. [7]

Так находим разделенные разности 1-го, 2-го... [8]

А - разделенные разности первого порядка, л: 0, узлы. [9]

Аналогично определяются разделенные разности более высокого порядка. [10]

Если алгоритм разделенных разностей не отказывает, то формула ( 23) дает каждый корень zk, который отличается по абсолютной величине от соседних с ним. [11]

При помощи разделенных разностей контролируется точность таблиц. Для этого составляют таблицы разделенных разностей различных порядков для соседних узлов и анализируют их поведение. [12]

Показать, что разделенные разности не изменятся, если аргументы увеличить на одну и ту же величину, а значения функции оставить неизменными. [13]

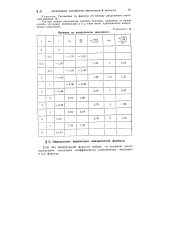Проверка на квадратичную зависимость. [14]

Так как вторая разделенная разность примерно постоянна, то можно считать, что между переменными л: и у имеет место приближенная квадратичная зависимость. [15]

Страницы: 1 2 3 4