Разделенная разность

Cтраница 2

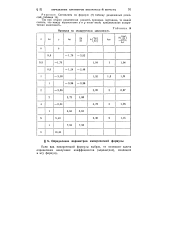Проверка на квадратичную зависимость. [16]

Так как вторая разделенная разность примерно постоянна, то можно считать, что между переменными х и у имеет место приближенная квадратичная зависимость. [17]

Данное определение оператора разделенной разности в ряде случаев конкретизируется. [18]

Ньютона требует вычисления разделенных разностей различных порядков, что усложняет расчеты, в то время как интерполяционный полином Лагранжа исключает подобные вычисления. [19]

Перечислим некоторые свойства разделенных разностей. [20]

Данное определение оператора разделенной разности в ряде случаев конкретизируется. [21]

Полученные нами выражения разделенных разностей с повторяющимися значениями аргументов слишком громоздки и не могут служить для практических вычислений. [22]

Эти величины называются разделенными разностями; при этом 2Л / 2 и 6Д аппроксимируют соответственно вторую и третью производные. [23]

Такие отношения называют разделенными разностями первого порядка. [24]

Эти отношения называют разделенными разностями второго порядка. [25]

Уп - д - разделенные разности различных порядков. Цри k 4 получаем новый алгоритм итерационной коррекции - метод кубичных парабол. [26]

Нетрудно видеть, что разделенные разности первого порядка не зависят от порядка аргументов в квадратных скобках. Покажем теперь, что это верно и для разделенных разностей второго порядка. [27]

Предполагаем, что все разделенные разности низшего порядка уже вычислены. Будем предполагать также, что под знаком разделенной разности имеется по крайней мере два различных аргумента. [28]

Как мы видим, разделенные разности второго порядка малы и разности более высоких порядков мы учитывать не будем. [29]

Обобщением понятия производной является понятие разделенной разности. [30]

Страницы: 1 2 3 4