Разрыв - скорость - перемещение
Cтраница 1
Разрыв скорости перемещения возможен только на линиях скольжения или их огибающих, иметь скачок может только касательная к линии разрыва составляющая скорости, нормальная составляющая - непрерывна. Скачок скорости не меняется вдоль линии скольжения. [1]
Поэтому линия разрыва скоростей перемещений совпадает с линией разрыва скоростей скольжения или в огибающей линии скольжения. [2]
Они показывают, что деформации на поверхности разрывов скоростей перемещений значительно превышают деформации частиц во внутренних точках пластической области. [3]
Можно показать, что в окрестности поверхности разрыва скоростей перемещения реализуется плоская деформация и ( 14) верно при условии ( 4) для общего случая пространственной деформации. [4]
Можно показать, что в окрестности поверхности разрыва скоростей перемещения реализуется плоская деформация и (1.15) верно при условии (1.4) для общего случая пространственной деформации. [5]
Затем из (6.91) - (6.94) устанавливаются поверхности разрыва скоростей перемещений на входе в матрицу и выходе из нее. [6]
Показано [21], что вдоль характеристических поверхностей возможны разрывы скорости перемещений, определяющих скольжение пластически деформированного тела вдоль границ жесткого состояния материала. [7]
С помощью (2.2) нетрудно получить (2.1) с учетом наличия поверхностей разрыва скоростей перемещений. [8]
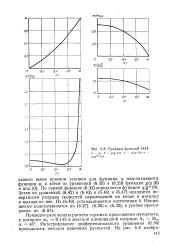 |
Графики функций. а - р. б - gig ( 0. в - w / w ( 0. г - X / g n ( 0. [9] |
Затем из уравнений (6.42) и (6.43) и (6.46) и (6.47) находятся поверхности разрыва скоростей перемещений на входе в матрицу и выходе из нее. [10]
В интеграл не включено касательное напряжение, так как проекция касательных сил на поверхности разрыва скоростей перемещений на ось х равна нулю. [11]
В интеграл не включены касательные напряжения, так как проекция на ось z касательных сил на поверхности разрыва скоростей перемещений равна нулю. Поясняя выражение (6.95), заметим, что 2яр р sin a cos a - площадь элемента сферической поверхности. [12]
Построенное решение справедливо в очаге деформации - в данном случае области, в которой соблюдается принятое выше предположение о радиальном течении материала в матрице. Очевидно, что очаг деформации ограничен двумя плоскостями матрицы и двумя поверхностями разрыва скоростей перемещений на входе в матрицу и выходе из нее. Для определения поверхностей разрыва скоростей перемещений необходимо вначале изучить течение материала в контейнере и калибрующем пояске. Поскольку оба эти течения описываются одинаковыми уравнениями, достаточно рассмотреть течение в контейнере. Vy vz 0, а скорость в направлении оси х не изменяется по этой оси vx V. Строго говоря, течение материала в контейнере является неустановившимся: скорость их зависит от координаты х и положения пресс-шайбы. [13]
Построенное решение справедливо в очаге деформации - в данном случае области, в которой соблюдается принятое выше предположение о радиальном течении материала в матрице. Очевидно, что очаг деформации ограничен конической поверхностью матрицы и двумя поверхностями разрыва скоростей перемещений на входе в матрицу и выходе из нее. Для определения поверхностей разрыва скоростей перемещений необходимо вначале рассмотреть течение материала в контейнере и калибрующем пояске, которые описываются одинаковыми по виду уравнениями. УР - vt - 0 а скорость в направлении оси z - vz не изменяется по этой оси. [14]
В условиях плоской деформации в связи с несжимаемостью идеального жесткопластического тела только один инвариант тензора Е является независимым ( например Е) и он может быть принят за характеристику величины деформации частицы. W, и величина W также может характеризовать величину деформации частицы при пересечении линии разрыва скоростей перемещений. [15]
Страницы: 1 2