Устранимый разрыв

Cтраница 1

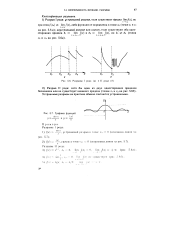Разрывы I рода ( а и II рода ( б.| Графики функций. [1]

Устранимые разрывы на практике обычно считаются устраненными. [2]

В точках устранимого разрыва или разрыва первого рода ( конечного скачка) первообразная непрерывна. При бесконечном разрыве f ( х) первообразная F ( х) может быть непрерывной или иметь разрыв. [3]

При наличии устранимого разрыва уравнения (1.4) и (1.5) не справедливы. [4]

В точке х устранимый разрыв, поскольку существует rnf ( х) rnx О. [5]

На практике точки устранимого разрыва встречаются при сосредоточенных распределениях физических величин. [6]

Точка хо называется точкой устранимого разрыва, если можно изменить значение функции только в этой точке ( или доопределить функцию в этой точке, если она в ней не определена) так, чтобы функция стала непрерывной в точке хо. [7]

Ясно, что точка устранимого разрыва является частным случаем точки разрыва первого рода и скачок функции в этой точке равен нулю. [8]

Точка а называется точкой устранимого разрыва функции у / ( ж), если предельное значение функции в этой точке существует но в точке а функция / ( ж) или не определена или ее частное значение / () в точке а не равно предельному значению. [9]

Тогда точка ха называется точкой устранимого разрыва. [10]

Таким образом, при ж5 функция имеет устранимый разрыв. [11]

Математика отмечает два случая разрыва функций: устранимый разрыв и неустранимый разрыв. [12]

Точка х - - 3 - точка устранимого разрыва. [13]

Точка 0 в этом случае называется точкой устранимого разрыва. Достаточно доопределить функцию f ( x) в точке х0, положив f ( 0) l, как разрыв устраняется. [14]

Точнее, Д имеет, быть можег, устранимые разрывы. [15]

Страницы: 1 2 3 4