Устранимый разрыв

Cтраница 3

Для устранения разрыва достаточно доопределить функцию, положив / ( 0) 1; б) в точке 0 устранимый разрыв. [31]

Функция у х A, tj -, х 3 ( ее график изображен на рис. 168) имеет устранимый разрыв. [32]

Для устранения разрыва достаточно доопределить функцию, положив / ( 0) 1; б) в точке 0 устранимый разрыв. [33]

Если / ( л о - 0) f ( x0 4 - 0), mo х называется точкой устранимого разрыва. [34]

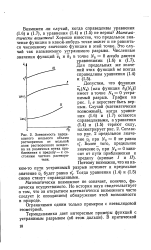Зависимость парциального мольного объема растворителя от мольной доли растворенного вещества на различных путях приближения к пределу - к состоянию чистого растворителя. [35]

Допустим, что функция v Nz) [ или функция / Zi ( JV2) ] имеет в точке N2 0 устранимый разрыв. График на рис. 1, б перестает быть верным. [36]

Ответ, х - - 2, х - - 3 - точки разрыва II рода, х - - 1 - точка устранимого разрыва. [37]

График этой функции изображен на. [38]

В этой же точке у ( - 0) 2 / ( 0) ф 2 / ( 0) Значит, х 0 - точка устранимого разрыва. [39]

В частности, если / ( a - f 0) f ( a - 0) / ( a), то точка а называется точкой устранимого разрыва. [40]

Равенство f ( xg - - Q) f ( xa - 0) означает, очевидно, что в точке х0 функция / или непрерывна, или имеет устранимый разрыв. Точка, в которой оба эти предела существуют, но не равны между собой, называется точкой разрыва первого рода, а разность / ( Jf0 0) - f ( x0 - Q) называется скачком функции / в этой точке. [41]

Если функция / не является непрерывной в точке х а и в то же время существует конечный предел Нтж а / ( х), то говорят, что она имеет устранимый разрыв в этой точке. Этим хотят сказать, что / можно видоизменить в точке а ( если она определена в а) или доопределить ее в этой точке ( если она в а не определена), положив / ( а) Нтж а / ( х), и после этого / станет непрерывной функцией в этой точке. [42]

Иногда выделяют случай, когда оба предела ( 1) существуют и равны, но / ( XQ -) / ( XQ) Ф / ( XQ) - Тогда точку XQ называют точкой устранимого разрыва. [43]

Производная ( дЕ / дп у т изменяясь вдоль критической кривой, не равна в пределе, в критической точке чистого растворителя, производной ( dEl / dnJyiT к т - е-претерпевает в критической точке чистого растворителя устранимый разрыв. [44]

II рода; е) д: 0 -точка разрыва I рода; ж) х - - точка разрыва I рода; з) х - 1 и х 3 -точки разрыва II рода; и) х1 - точка устранимого разрыва; к) х - 1-точка разрыва I рода; л) х - 1 - точка разрыва I рода. [45]

Страницы: 1 2 3 4