Расположение - корень
Cтраница 1
Расположение корней 1 KGH определяет устойчивость системы. [1]
Расположение корней обоих уравнений можно представить очень наглядно, если воспользоваться графическим изображением. [2]
 |
Оценка качества сиетемы автоматического регулирования. [3] |
Расположению корней в этой области соответствует обеспечение требуемого запаса устойчивости, определяемого величиной коэффициента колебательности т или степенью затухания г) и требуемой степенью устойчивости т ], характеризующей быстродействие системы. [4]
Определить расположение корней полинома с комплексными коэффициентами ( знаки вещественных частей корней) можно при помощи теоремы Эрмита - Билера [56 ], а также критериев Найквиста или Михайлова. [5]
 |
S. 4. Последовательность операций получения преобразования однополюсного сигнала, модулирующего синусоидальную несущую. [6] |
График расположения корней показан на рис. 18.3, г. Полюса н нули С используются без изменений, а полюса С вводятся как нули, и наоборот. Нули модуляции расположены влево от немодулированных нулей и на несколько более высокой частоте. [7]
Схема расположения корней в комплексной плоскости показана на рие. [8]
Исследованию расположения корней таких квазиполиномов и посвящается этот параграф. Квазиполином является целой аналитической функцией. [9]
Характер расположения корней уравнения ( 6) § 3.4, описывающего глобальные возмущения при 1 1 ( когда они локализуются вблизи от границы шара rR), можно выяснить так же, как и выше. [10]
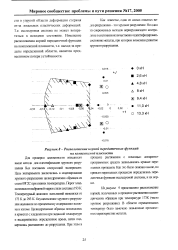 |
Расположение корней передаточных функций на комплексной плоскости. [11] |
Изменение расположения корней передаточной функции на комплексной плоскости, т.е. выход за пределы определенной области, является предвестником потери устойчивости. [12]
Анализ расположения корней характеристического уравнения (7.2.5) на комплексной плоскости составляет чисто алгебраическую задачу. Для развертывания характеристического определителя существует ряд оригинальных методов. С использованием этих методов средства вычислительной техники позволяют непосредственно находить коэффициенты характеристических полиномов сколь угодно высокой степени с наперед заданной точностью. Остаются весьма полезными критерии, которые могли бы давать ответ о размещении корней на комплексной плоскости, не прибегая к решению полной задачи о собственных значениях. [13]
При расположении корней класса О функция h ( t) монотонная. [14]
Вопрос о расположении корней уравнения ( II) может быть решен с помощью критерия Рауса - Гурвица или критерия Михайлова. [15]
Страницы: 1 2 3 4