Распределение - дисперсия
Cтраница 1
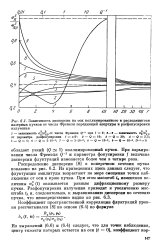 |
Зависимость дисперсии на оси коллимированного и расходящегося. [1] |
Распределение дисперсии [8] в поперечном сечении пучка покдзано на рис. 6.2. Из приведенных здесь данных следует, что флуктуации амплитуды возрастают по мере смещения точки наблюдения от оси к краю пучка. [2]
Поэтому распределение дисперсии ошибок имеет плавную низкочастотную огибающую. [3]
График распределения дисперсий по частотам называют спектром процесса с периодическими реализациями. [4]
При таком распределении дисперсий общая стоимость элементов получится на 25 % меньшей, чем у аналогичного устройства, в котором, как это иногда делают, применены равноточные элементы. [5]
 |
Обработка ( NxN изображения чайных величин равняется а2. Тогда ковариационные матрицы для строк и столбцов можно записать как I [ CM. выражения, ( П8. и ( П8. ]. [6] |
Затем вычисляется функция распределения дисперсии a2 ( w, v) как функция величин 2i ( s, s) и 22 ( 5 5), которые являются диагональными элементами Si и 22 соответственно. [7]
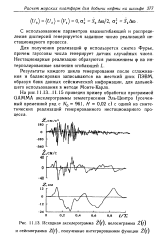 |
Исходная акселерограмма Z ( t, велосиграмма Z ( t и сейсмограмма Z ( t, полученные интегрированием функции Z t. [8] |
С использованием параметров квазиогибающей и распределения дисперсий генерируется заданное число реализаций нестационарного процесса. [9]
Спектральная плотность случайного процесса характеризует распределение дисперсий по частотам спектра с выделением превалирующих частот. [10]
Спектральный состав исследуемого случайного процесса описывает распределение дисперсий по различным частотам. [11]
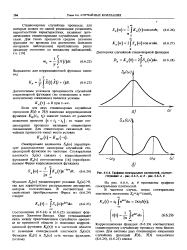 |
Графики спектральных плотностей, соответствующие. а - рас., а. б - , б. [12] |
Спектральная плотность З со) характеризует распределение дисперсии случайной стационарной функций по частотам. [13]
В практических приложениях используются также характеристики распределения дисперсии случайной функции X ( t) по спектру частот. Этой характеристикой служит спектральная плотность случайной функции. Согласно теореме Винера-Хин - чина имеем следующие формулы, связывающие корреляционную функцию К. [14]
Функция плотности спектра мощности ( ПСМ) определяет распределение дисперсии ( среднеквадратичного значения) временной последовательности по частотам. Своим происхождением термин обязан электротехнике. [15]
Страницы: 1 2 3