Распределение - дисперсия
Cтраница 3
При анализе стационарных случайных процессов используются спектральные характеристики, связанные со следующими понятиями из теории колебаний. По аналогии со спектром колебательного процесса спектр стационарной случайной функции описывает распределение дисперсий по различным частотам. Спектральное разложение случайной функции состоит из гармонических колебаний различных частот, а амплитуды колебаний являются случайными величинами. [31]
 |
Распределение 2ь ( з, s / a2 по коэффициентам для различных преобразований. [32] |
Так как эта матрица симметрична, то приводится только ее верхняя треугольная часть. Из приведенной матрицы следует, что двумерные дисперсии в случае дискретного косинусного преобразования представляют собой функцию распределения дисперсии, имеющую максимум в начале координат, обладающую круговой симметрией и монотонно убывающую по величине по мере увеличения пространственных частот. [33]
 |
Зависимость процента ЭКГ с отклонениями, классифицированных как нормальные, от числа сохраняемых признаков при тождественном преобразовании ДКП и ПУА, упорядоченным по Адамару. [34] |
В данной главе приведены некоторые простые алгоритмы классификации и методы их реализации. Применение таких алгоритмов и связанное с ними эффективное понижение размерности при выборе признаков основываются на дисперсионном критерии и распределении дисперсии. [35]
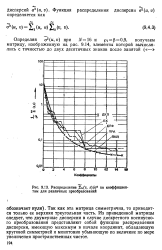
Графическим представлением дисперсионного критерия является график дисперсий коэффициентов преобразования, где дисперсии расположены в порядке убывания и нормированы к следу 1 матрицы Sec или Sy. Такой график называется графиком распределения дисперсии. На рис. 9.1 приведено распределение дисперсии, связанное с четырьмя различными преобразованиями. Площадь, ограниченная каждой кривой для заданного числа коэффициентов. Общая площадь, ограниченная каждой кривой, равняется единице в результате нормировки на след. Например, при сохранении 20 коэффициентов из рис. 9.1 следует, что преобразования упорядочиваются по эффективности следующим образом. [36]
 |
Разложение эргодического случайного процесса ( а на гармоники ( б, в, г с детерминированными частотами и случайными амплитудами. [37] |
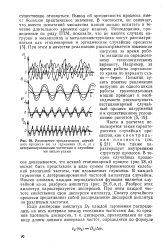
В каждой гармонике с детерминированной частотой амплитуды случайны. Разброс этих амплитуд характеризуется дисперсией. При этом каждой частоте свойственна своя дисперсия амплитуд. Спектр случайного процесса представляет собой распределение дисперсий амплитуд по различным частотам. [38]
 |
Восстановление помощью ОДКП. [39] |
Затем вычисляется обратное дискретное косинусное преобразование и результирующая ЭКГ записывается с помощью графопостроителя. Потеря информации, связанная с использованием сжатия в соотношении 3: 1 с помощью дискретного косинусного преобразования, незначительна. Оставляемые 43 коэффициента перечислены в табл. 9.3.2. Дисперсионный критерий и распределение дисперсии можно эффективно использовать для сжатия данных. [40]
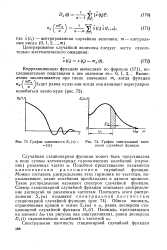 |
График зависимости / С. т ( т / ( т.| График спектральной плот-ности случайной функции. [41] |
Случайная стационарная функция может быть представлена в виде суммы элементарных гармонических колебаний ( гармоник) различных частот о. Подобное представление называется каноническим разложением случайной функции. Можно составить распределение этих гармоник по частотам, показывающее, какие колебания преобладают в данном процессе. Такое распределение называют спектром случайной функции. Спектр стационарной случайной функции описывает распределение дисперсий по различным частотам. [42]
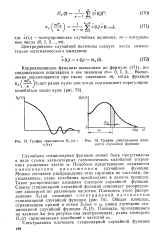 |
График зависимости / С ( т [ IMAGE ] График спектральной плот - / ( т ности случайной функции. [43] |
Случайная стационарная функция может быть представлена в виде суммы элементарных гармонических колебаний ( гармоник) различных частот со. Подобное представление называется каноническим разложением случайной функции. Можно составить распределение этих гармоник по частотам, показывающее, какие колебания преобладают в данном процессе. Такое распределение называют спектром случайной функции. Спектр стационарной случайной функции описывает распределение дисперсий по различным частотам. [44]
В этом месте мне необходимо привести некоторые оговорки. Когда я заявляю, что рынок характеризуется бесконечной дисперсией, я не имею в виду, что дисперсия действительно бесконечна. Как и во всех фрактальных структурах, здесь, в конечном счете, есть интервал времени, в котором фрактальное масштабирование перестает работать. В предыдущих главах я говорил, что деревья представляют собой фрактальные структуры. Мы знаем, что ветви дерева не становятся бесконечно малыми. Аналогично, для рыночных прибылей мог бы существовать объем выборки, где дисперсия, действительно, становится конечной. Следовательно, для всех практических целей рыночные прибыли будут вести себя, как будто они являются бесконечными распределениями дисперсии. По крайней мере, мы можем предположить, что в пределах нашей жизни они будут вести себя, как будто они имеют бесконечную дисперсию. [45]
Страницы: 1 2 3