Распределение - дисперсия
Cтраница 2
 |
Блок-схема стенда для испытаний на случайную вибрацию. [16] |
Важнейшей характеристикой случайной вибрации является спектральная характеристика - распределение дисперсии ускорения по частотам. При испытаниях обычно стремятся обеспечить постоянство спектральной характеристики. [17]
Авторы [35] с помощью соотношений канонического разложения получают выражения для распределения дисперсии и спектральной плотности пульсаций в различных точках пластины. [18]
 |
Распределение дисперсии. [19] |
Ниже, на примере обработки электрокардиограмм, будет показано, как распределение дисперсий используется для сжатия данных. [20]
Наличие ротатабельности устраняет второй недостаток клас сического регрессионного анализа - неравномерность распределения дисперсии в изученной области факторного пространства. [21]
Кривая Sx ( to) ( рис. 79) изображает плотность распределения дисперсий по частотам непрерывного спектра. [22]
Спектр мопщости шума является одной из наиболее важных характеристик, так как оценивает распределение дисперсии шума по частотам. Если известна такая характеристика для конкретных приемников, можно вь1брать оптимальную частоту модуляции сигнала и полосу пропускания систем ] ь1 и тем самым значительно улучшить эффективность измерений. [23]
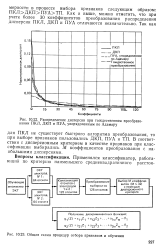 |
Распределение дисперсии при тождественном преобразовании ПКЛ, ДКП и ПУА, упорядоченным по Адамару.| Общая схема процедур отбора признаков и обучения. [24] |
Как и выше, можно отметить, что при учете более 30 коэффициентов преобразования распределения дисперсии ПКЛ, ДКП и ПУА отличаются незначительно. [25]
Функция х ( д) удовлетворяет условию Sx ( co) 0, так как характеризует распределение дисперсии, которая положительна. [26]
Расчет дисперсии предсказанного значения параметра оптимизации в случае уравнений регрессии, полученных по пассивным планам, - задача крайне трудная вследствие сложности ковариационной матрицы и неравномерности распределения дисперсии в факторном пространстве. Эта задача существенно упрощается при использовании ротатабельных планов. [27]
Мы видим, что с увеличением периода разложения ( 7 - - оо) ступенчатая функция 5 ( сой) будет неограниченно приближаться к плавной кривой 5 ( ю), которая представляет собой плотность распределения дисперсий по частотам непрерывного спектра. [28]
Это объясняется тем, что в качестве стационарной случайной функции часто рассматриваются такие величины, как ток и напряжение. Тогда распределение дисперсий, имеющих квадрат размерности амплитуды сигнала, пропорционально плотности распределения энергии сигнала по частотам. [29]
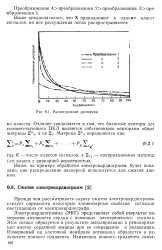
Графическим представлением дисперсионного критерия является график дисперсий коэффициентов преобразования, где дисперсии расположены в порядке убывания и нормированы к следу 1 матрицы Sec или Sy. Такой график называется графиком распределения дисперсии. На рис. 9.1 приведено распределение дисперсии, связанное с четырьмя различными преобразованиями. Площадь, ограниченная каждой кривой для заданного числа коэффициентов. Общая площадь, ограниченная каждой кривой, равняется единице в результате нормировки на след. Например, при сохранении 20 коэффициентов из рис. 9.1 следует, что преобразования упорядочиваются по эффективности следующим образом. [30]
Страницы: 1 2 3