Распределение - долговечность
Cтраница 1
Распределение долговечности при постоянном уровне напряжений подчиняется логарифмически нормальному закону; для умеренных температур возможно существование порогов чувствительности ( см. стр. [1]
 |
Структурные изменения под дорожкой.| Зависимость силы деформирования Р от степени пластической деформации Е. [2] |
Распределение долговечностей одинаковых подшипников, отработавших в идентичных условиях, близко к законам логарифмически нормальному и Вейбулла. Ниже приводятся некоторые сведения о графической интерпретации контактной долговечности подшипников или образцов металла, испытанных ( или отработавших) в идентичных условиях. [3]
Функции распределения долговечности при этом получаются методом перемножения стохастических матриц и методом Монте-Карло. [4]
По кривой распределения долговечности определяется время, когда начнутся первые замещающие продажи. На фактическое время замещения оказывают влияние экономическое положение клиента, наличие у него средств и возможности выбора альтернативного товара, а также установленные компанией цены, условия оплаты и предпринимаемые ею усилия по организации сбыта. Поскольку объем замещающих продаж трудно оценить до начала эксплуатации товара, некоторые производители основывают свои решения о выходе на рынок с новым товаром исключительно на оценках объема первичных продаж. [5]
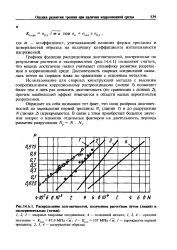 |
Распределение долговечностей, полученное расчетным путем ( линии и экспериментально ( точки. [6] |
Графики функции распределения долговечностей, построенные по результатам расчетов и экспериментов ( рис. 14.6.1) позволяют считать, что модель достаточно полно учитывает специфику развития разрушения в коррозионной среде. [7]
Эмпирическая функция распределения долговечности строится обычно на логарифмически нормальной вероятностной бумаге. [8]
Задавая функцию распределения долговечности F ( t), расчет по формуле ( 4) выполняется с помощью ПЭВМ с использованием известных численных методов. [9]
Анализируется бимодальный закон распределения долговечности конструкционных материалов при действии переменных напряжений с постоянной амплитудой. Проведено сравнение расчетных и экспериментальных зависимостей числа циклов до разрушения при сложном нагружении, когда напряжения с высокой частотой накладываются на циклически изменяющееся напряжение с постоянной амплитудой и заданной асимметрией циклической нагрузки. [10]
Для дальнейшего анализа функции распределения долговечности вычисленные значения долговечности целесообразно представить в виде вариационного ряда с последующим построением на логарифмической нормальной вероятностной бумаге [5] графика функции распределения. [11]
 |
Процессы накопления повреждений. [12] |
Значительный интерес представляет выяснение закона распределения долговечности. Получим асимптотическую ( при большом числе нагружений) оценку этого закона. [13]
Получим теперь асимптотическую оценку закона распределения долговечности при большом числе нагружений. [14]
Поэтому необходимо также экспериментально-теоретически обосновывать функции распределения долговечностей в зависимости от уровня напряжений, а также разрабатывать температурно-временные зависимости прочности по параметру вероятности разрушения. [15]
Страницы: 1 2 3 4 5