Распределение - долговечность
Cтраница 4
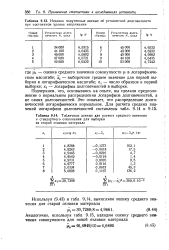
В качестве примера на рис. 5.3 кривыми /, 2, 3 представлены полученные таким образом функции распределения долговечности образцов при регулярном нагружении при испытании на плоский изгиб при трех уровнях амплитуд напряжений. [46]
В связи со статистической природой усталости важнейшими характеристиками, используемыми при оценке надежности конструкций на основе вероятностных представлений, являются параметры распределения долговечностей и пределов выносливости. Эти характеристики получают экспериментально путем испытаний на усталость. Необходимость статистической обработки результатов вызывает многократное увеличение количества объектов испытаний и их общей продолжительности. [47]
Подсчитав затем значения 1А и Sa, а также суммарное среднее квадратическое отклонение S SL по уравнению ( 99), получаем итоговое распределение долговечности. [48]
Зная доверительные интервалы для х и s, наносят границы доверительной области, которая с вероятностью Р накладывается на линию, соответствующую теоретической функции распределения долговечности. [49]
Объем имеющейся экспериментальной информации о характеристиках прочности и нагруженности определяет уровень достоверности ( доверительные интервалы) оценки средних значений и показателей рассеяния указанных величин, а следовательно, и функции распределения долговечности детали, рассчитываемой на их основе. [50]
Если в детали возникает плоское напряженное состояние с компонентами а ( нормальное напряжение) и т ( касательное напряжение), причем ант являются случайными функциями времени, то расчет функции распределения долговечности может быть основан на следующих предпосылках. [51]
Если в детали возникает плоское напряженное состояние с компонентами о ( нормальное напряжение) и т ( касательное напряжение), причем акт; являются случайными функциями времени, то расчет функции распределения долговечности мо жет быть основан на следующих предпосылках. [52]
Опыт практических расчетов показывает, что подбор по эмпирическим функциям распределения амплитуд некоторых непрерывных функций для их описания и последующего использования интегральных формул при расчете функций распределения усталостной долговечности является менее предпочтительным методом по сравнению со ступенчатой аппроксимацией непосредственно эмпирических распределений и расчетом распределения долговечности по описанной выше методике. В этом методе учтено постепенное снижение предела выносливости вследствие циклических перегрузок. Результаты оценки весьма близки к результатам, полученным на основе корректированной линейной гипотезы суммирования усталостных повреждений. [53]
При длительных статических испытаниях образцов при постоянном напряжении неоднородность материала проявляется в разбросе долговечности. Распределение долговечности удовлетворительно описывается законом Вейбулла и логарифмически нормальным. [54]
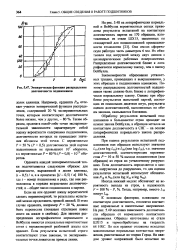 |
Эмпирическая функция распределения долговечности подшипников. [55] |
Закономерности образования усталостных трещин, приводящих к выкрашиванию, у этих образцов и подшипников одинаковы. Поэтому распределение долговечностей подшипников также должно быть ближе к логарифмически нормальному закону. Однако при обработке результатов испытаний партий, состоящих из нескольких десятков штук, результаты оценок долговечностей, выполненных по обоим законам, оказываются близкими. [56]
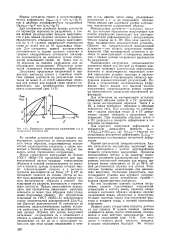 |
Диаграммы предельных напряжений ( и в. [57] |
Для построения семейства кривых усталости по параметру вероятности разрушения, а также кривой распределения предела выносливости и для оценка среднего значения и среднего квадратичного отклонения предела выносливости на 4 - 6 уровнях напряжений испытывают серии не менее чем из 10 одинаковых образцов. Для построения кривой распределения долговечности и оценки среднего значения и среднего квадратичного отклонения логарифма долговечности на заданном уровне напряжений испытывают серию не менее чем из 10 образцов до полного разрушения или до образования макротрещин. Результаты испытаний подвергают статистической обработке. [58]
Данная методика была применена при расчете рам тележек локомотивов [4, 35] и электровозов [17], полуосей [37] и рам автомобилей, лопастей вертолетов, ряда деталей сельскохозяйственных, металлургических [9] и других машин. Полученные расчетом функции распределения долговечности оказались в хорошем соответствии с данными об эксплуатационных отказах по усталостному разрушению. [59]
Страницы: 1 2 3 4 5