Распределение - долговечность
Cтраница 2
 |
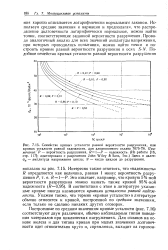
Кривые распределения долговечностей материала ( 33 - 18С при длительном статическом нагружении. [16] |
Проведение статистической обработки требует знания закона распределения долговечностей. [17]
Аналогично могут быть вычислены и другие моменты распределения долговечности. [18]
Аналогично могут быть записаны и другие моменты распределения искомой долговечности. [19]
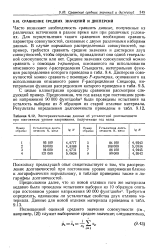 |
Экспериментальные данные об усталостной долговечности при постоянном уровне напряжения, полученные год назад. [20] |
Поскольку предыдущий опыт свидетельствует о том, что распределение долговечностей при постоянном уровне напряжения близко к логарифмически нормальному, в таблице приведены также и логарифмы долговечностей. [21]
Таким образом, допущение о логарифмически нормальном законе распределения долговечности вполне обосновано. [22]
В ряде случаев возникает необходимость оценки параметров функции распределения долговечности без использования ЭВМ, для чего применяют следующий метод. [23]
По результатам стендовых и эксплуатационных испытаний построена функция распределения долговечности рамы, которая позволяет прогнозировать долговечность рам опытных конструкций. Для новых автомобилей МАЗ-5336 ожидаемая долговечность рамы составляет 400 тыс. км пробега. [24]
Используя средние значения и вариации и предполагая, что распределение долговечности логарифмически нормальное, можно найти точки, соответствующие заданной вероятности разрушения. [26]
Проблема второго типа возникает при эксплуатации системы, функция распределения долговечности которой известна в одной точке. Самостоятельной индикации отказа в данном случае в системе не происходит, поэтому для обнаружения отказа в ожидаемые моменты времени проводятся проверки. Эксплуатация системы длится либо до момента обнаружения отказа, либо до некоторого назначенного момента. [27]
В рамках предлагаемой стратегии эксплуатации аппаратов и сосудов функция распределения долговечности определяется на одном из этапов расчета индивидуального остаточного ресурса. Задача разработки оптимального плана проверок решается при наличии информации об уровне надежности технических систем. [28]
Проблема третьего типа возникает в случаях, когда известна функция распределения долговечности ( остаточного ресурса) обследуемой технической системы. Здесь используются традиционные вероятностно-статические методы моделирования надежности сложных технических систем. [29]
Для элементов радиоэлектронной аппаратуры, у к-рых преобладают внезапные отказы, распределение долговечности часто является экспоненциальным. [30]
Страницы: 1 2 3 4 5