Распределение - интервал - время
Cтраница 2
 |
Зависимость интенсивности отказов от времени эксплуатации аппаратурных ( 1 и программных ( 2 средств. [16] |
Рассмотрим основные характеристики потока отказов, базирующиеся на законе распределения интервала времени между отказами. [17]
Из проведенного анализа видно, что задачи о нахождении распределений интервалов времени между соседними нулями и соседними экстремумами к настоящему времени не имеют точных эффективных решений. [18]
Функция о ( /) может теперь быть истолкована просто как распределение интервала времени между последним мгновением, когда еще наблюдается состояние нуль, и первым мгновением, когда оно наблюдается вновь. [19]
Импульсные потоки случайных воздействий могут быть полностью описаны распределением интенсивности импульсов и распределением интервалов времени между ними. Получение эмпирических рядов для этих распределений обычно не встречает больших трудностей, а подбор для них соответствующего теоретического закона распределения сводится к применению обычных методов математической статистики. [20]
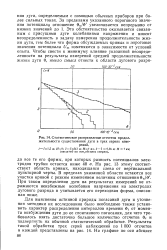 |
Статистическое распределение отсчетов продолжительности существования дуги в трех сериях измерений. [21] |
Для выяснения истинной природы погасаний дуги и уточнения методики их исследования было необходимо также установить характер распределения интервалов времени О от момента возбуждения дуги до ее спонтанного погасания, для чего требовалось взять достаточно большое количество отсчетов Qi и подвергнуть их обычной статистической обработке. [22]
Из соотношения (11.76), в частности, следует, что отыскание распределения раз-махов может быть сведено к определению распределения интервалов времени между соседними экстремумами, что в значительной степени упрощает обработку экспериментальных данных. [23]
Получая от датчика случайных величин случайные числа Ri, распределенные в интервале 0 - 1, можно по функциям распределения интервалов времени до аварии F T) и длительности времени восстановления F ( t) получить TI и t для данной реализации. [24]
Некоторые результаты анализа трех отличающихся по сложности структуры процессов, имеющих корреляционные функции типа (4.136) приведены на рис. 4.10 - 4.12: а - корреляционная функция; б - спектральная плотность; в - плотность распределения интервала времени между соседними экстремумами; г - плотность распределения максимумов; д, е - среднее значение и стандарт абсолютного максимума; ж - плотность распределения половин размахов. [25]
Пусть р9 ( л: 0 / 0, X-L / Г) - совместная плотность распределения двух соседних экстремумов при условии, что они разделены интервалом времени т, а р ( т) - плотность распределения интервала времени между соседними экстремумами. [26]
В данной главе принята точка зрения, что для правильного выбора плана статистических испытаний необходимо решить три главнейших вопроса: 1) определить партию изделий, при помощи которой будет приниматься решение; 2) определить подходящую модель распределения интервалов времени между отказами и 3) выбрать план испытаний из имеющихся планов, основанных на принятом распределении. Ниже рассматриваются все эти вопросы, и там, где это возможно, предлагаются методы выбора требуемых решений. [27]
В данной главе принята точка зрения, что для правильного выбора плана статистических испытаний необходимо решить три главнейших вопроса: 1) определить партию изделий, при помощи которой будет приниматься решение; 2) определить подходящую модель распределения интервалов времени между отказами л 3) выбрать план испытаний из имеющихся планов, основанных на принятом распределении. Ниже рассматриваются г. се эти вопросы, и там, где это возможно, предлагаются методы выбора требуемых решений. [28]
Распределения интервалов времени между поступающими заявками каждого типа в крайних случаях можно принять либо постоянными ( регулярные периодические потоки), либо случайными, образующими простейшие ( пуассоновские) потоки. [29]
Распределение интервалов времени между отдельными сообщениями, поступающими в ЦВМ A ( t), целиком определяется спецификой данной управляющей системы и требует предварительного изучения в каждом конкретном случае. В ряде случаев распределение моментов времени поступления сообщений оказывается близким к пуас-соновскому [1.5] или эрланговскому [1.19] и допускает предположение о стационарности и отсутствии последействия. [30]
Страницы: 1 2 3