Распределение - корень
Cтраница 2
Более детальное исследование распределения корней характеристического уравнения позволяет сделать оценку качественных показателей рассматриваемой системы более подробно. [16]
Ограничения на показатели распределения корней характеристического уравнения системы вне зависимости от свойств канонического базиса должны выдерживаться в каждой из эквивалентных сепаратных систем. [17]
Для систем с распределением корней 2-го и более высоких классов выражения для оценок качества переходных процессов получаются чрезмерно сложными и не имеют практпч. [18]
Для систем с распределением корней 2-го и более высоких классов выражения для оценок качества переходных процессов получаются чрезмерно сложными и не имеют практич. [19]
Для более точного описания распределения корней представим любой член квазиполинома zpe - TZ в виде е1п г т % следовательно, гре - Т2 еР 1п 121 - т Кег. Отсюда видно, что zpe T2 является монотонно возрастающей функцией р In z - т Re z, и если в каком-нибудь квазиполиноме при z - - оо по какому-нибудь направлению arg z const, или по какому-нибудь иному закону возрастания z z ( t), для одного члена квазиполинома значение и. In z - т Re z больше аналогичного выражения для других членов, то в этом направлении arg z const или вдоль данной кривой z z ( t) при z - оо не может быть нулей квазиполинома. [20]
В других вариантах методов распределения корней задаются значениями корней. [21]
И, К задаче распределения корней полиномов, ДАН СССР, нов. [22]
 |
Определение распределения корней по. - кривой. [23] |
При этом считается, что распределение корней для какой-либо одной области было первоначально найдено тем или иным способом. [24]
В этой книге мы рассматриваем распределение корней уравнения / ( z) а для различных значений а и функций / ( z) и, в частности, сравнительные скорости роста N ( r, a), когда а пробегает комплексную плоскость. [25]
 |
Пример. Дано уравнение. [26] |
После этого требуется дополнительное исследование распределения корней внутри одной из нанесенных областей или на их границе. При этом достаточно найти распределение корней в произвольной одной точке плоскости параметров - во всех остальных точках распределение корней позволит установить штриховка. Поясним сказанное на примере. [27]
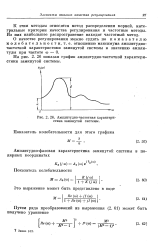 |
Амплитудно-частотная характеристика замкнутой системы. [28] |
К этим методам относятся метод распределения корней, интегральные критерии качества регулирования и частотные методы. Из них наибольшее распространение находит частотный метод. [29]
Косвенные методы анализа ( нахождение распределения корней характеристического уравнения системы, интегральный метод, частотный метод и др.) позволяют избавиться от громоздких вычислительных операций. [30]
Страницы: 1 2 3 4