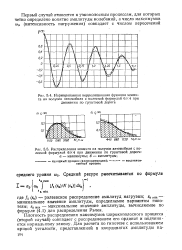
Распределение - максимум
Cтраница 1
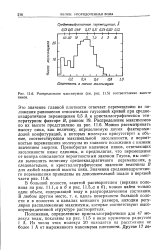 |
Распределение максимумов ( соответственно высоте пиков. [1] |
Распределение максимумов по их высоте представлено на рис. 11.6. Можно рассматривать высоту пика, как величину, определяемую двумя факторами: долей конфигураций, в которых молекула присутствует в объеме, соответствующем максимальной заселенности, и вероятностью перемещения молекулы из главного положения с низким значением энергии. Пренебрегая наличием пиков, отвечающих заселенности ниже единицы, и предполагая, что перемещение от центра описывается вероятностным законом Гаусса, мы смогли вычислить величину среднеквадратичного перемещения, а следовательно, и кристаллографическое значение величины В для любой заданной высоты пика. [2]
 |
Связь между рентгенограммой и распределением полюсов на сфере проекций в общем случае. [3] |
Распределение максимумов на дифракционном кольце будет точно повторять собой распределение максимумов на кольце нормалей UV. Рентгенограмма будет подобна срезу сферы проекций плоскостью, перпендикулярной рентгеновскому лучу. [4]
Распределение максимума гауссовского процесса / / Теория вероятн. [5]
Характер распределения максимумов зависит от отношения расстояния между источниками к длине волны. [6]
Плотность распределения максимумов широкополосного процесса ( второй случай) совпадает с распределением его ординат и подчиняется нормальному закону. [8]
Сформулируем наш результат относительно распределения максимума (6.11), которое согласно (6.12) есть предельное распределение для интересующего нас времени ожидания ffln при п - - оо. [9]
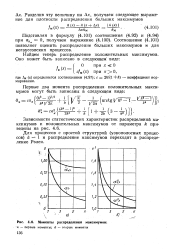 |
Моменты распределения максимумов. [10] |
Соотношение (4.101) позволяет оценить распределение больших максимумов и для негауссовских процессов. [11]
 |
Схемы к пояснению метода максимумов ( а и метода учета одного экстремума между двумя соседними пересечениями среднего уровня ( б. [12] |
На практике в большинстве случаев распределение максимумов симметрично распределению минимумов относительно среднего уровня ат, В этом случае методы максимумов и экстремумов приводят к весьма близким функциям распределения амплитуды. [13]
Если ( Зя1, то распределение максимумов приближенно следует распределению Ре-лея. [14]
Устойчивая, не изменяющаяся со временем интерференционная картина - распределение максимумов и минимумов поля - возникает лишь в том случае, если налагающиеся волны имеют одинаковый период и неизменный сдвиг фаз в каждой точке. [15]
Страницы: 1 2 3 4