Распределение - больцман
Cтраница 2
Распределение Больцмана может быть выведено еще и совсем иным способом, непосредственно из условия максимальности энтропии газа в целом, рассматриваемого как замкнутая система. Этот вывод представляет существенный самостоятельный интерес, поскольку он основан на методе, дающем возможность вычислить энтропию газа, находящегося в п-роизвольном неравновесном макроскопическом состоянии. [16]
Используя распределение Больцмана ( см. задачу 2.100), найти при температуре Т отношение a - n i ( Nn i / ( Nn), где ( Nk - среднее число осцилляторов на k - ом уровне энергии. [17]
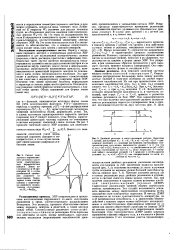
Это распределение Больцмана дает плавное изменение интенсивности, относительно которого четные и нечетные состояния чередуются по интенсивности ( фиг. [18]
Применим распределение Больцмана к газу, находящемуся в поле земного тяготения. [19]
Определяющая распределение Больцмана связь между населенностью уровней и темп-рой обобщена на случай неравновесных населенностей. [21]
Использование распределения Больцмана справедливо в том случае, когда предполагается наличие частиц, находящихся в различных энергетических состояниях и способных к взаимному переходу из одного состояния в другое. Таким требованиям отвечал бы частично расплавленный кристалл, который был бы образован беспорядочно расположенными кристаллическими и некристаллическими участками цепей. Хираи исходит из иной модели. [22]
Закон распределения Больцмана приложим к системам бозонов или фермионов при высоких температурах. При более низких температурах, когда число поступательных состояний с энергией, не превышающей 3 / 2 kT, почти равно числу молекул, наблюдается отклонение от этого распределения, поскольку различные веса приписываются состояниям с двумя или несколькими молекулами на одном и том же уровне. Истинный закон для бозонов называется законом распределения Бозе - Эйнштейна, а закон для фермионов называется законом распределения Ферми - Дирака. Некоторые свойства жидкого 4Не и жидкого 3Не, состоящих соответственно из бозонов и фермионов, подтверждают указанные выше отклонения от распределения Больцмана. [23]
Формула распределения Больцмана ( 262) получается следующим путем. [24]
Между распределениями Больцмана и А1аксвелла имеется большое сходство: и в том и в другом случае основным множителем является экспонента, под знаком которой стоит отношение энергии молекулы ( в одном случае потенциальной, в другом кинетической) к величине kT, определяющей среднюю энергию теплового движения молекул. [25]
Между распределениями Больцмана и Максвелла имеется большое сходство: и в том и в другом случае основным множителем является экспонента, под знаком которой стоит отношение энергии молекулы ( в одном случае потенциальной, в другом кинетической) к величине kT, определяющей среднюю энергию теплового движения молекул. [26]
Следовательно, распределение Больцмана использует ся для свободных молекул газа, а распределение Ферми - Дирака для электронов проводимости ( или дырок) в твердом теле. [27]
Применим теперь распределение Больцмана к частному слу чаю одноатомного газа. [28]
Из соотношения распределения Больцмана, приведенного выше, можно видеть, что легкость возбуждения находится в соответствии с различием в энергии между основным и возбужденным состоянием атома. Отсюда следует, что в большинстве случаев пламенно-эмиссионная спектрометрия более чувствительна для определения элементов, имеющих резонансные спектральные линии между 400 и 800 нм, в то время как атомно-абсорбционная спектрометрия более чувствительна для определения элементов, линии которых лежат между 200 и 300 нм. [29]
С помощью распределения Больцмана рассчитывается поляризация полярных диэлектриков и намагничение парамагнетиков. [30]
Страницы: 1 2 3 4