Распределение - перемещение
Cтраница 1
Распределение перемещений при использовании вариационного принципа (4.184) не связано с распределением напряжений и выбирается независимо от него. [1]
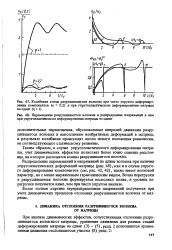
Распределение перемещений и напряжений по длине волокна при наличии упругопластических деформаций матрицы ( рис. 48), как и в случае упругого деформирования компонентов ( см. рис. 42, 43), также имеет волновой характер, но с менее выраженным гармоническим видом. Волна перегрузки в разрушившемся волокне формируется несколько позже, и уровень перегрузки получается ниже, чем при чисто упругом анализе. [3]
Распределения перемещений и напряжений по координате и времени представлены на рисунках 2.4.1 и 2.4.2. На рис. 2.4.3 показана зависимость напряжений от пространственной координаты в различные моменты времени. [4]
Распределение перемещений при использовании вариационного принципа (4.184) не связано с распределением напряжений и выбирается независимо от него. [5]
Рассмотрим подробно распределение перемещений по толщине трехслойного пакета. [6]
Значит, распределение перемещений, скоростей частиц и деформаций по длине стержня со свободными концами в один и тот же момент времени имеет вид, показанный на рис. 182, а, причем распределение напряжений подобно распределению деформаций. [7]
Такая форма распределения перемещений соответствует приводимым ниже выражениям (6.12), которые были определены для тонкой цилиндрической оболочки, выпучивающейся при осевом сжатии. Определены также амплитуды перемещений в, у, w, которые приводятся в таблице 6.4 ( при pq - 11 они соответствуют первой, или фундаментальной, гармонической составляющей), подтверждается высказанное выше преположение об относительных величинах этих перемещений в цилиндрической оболочке. В других типах оболочек перемещения и могут и не быть меньше, чем перемещения v, но оба они будут существенно меньше, чем перемещения w, в таких распространенных случаях, как расчет на прочность при поперечном нагружении или исследование потери устойчивости. [8]
Пространственно-временные картины распределения перемещения и ( х т) и напряжения сг ( ж т) представлены на рисунках 2.3.2 и 2.3.3, на которых отчетливо прослеживается стремление решения с течением времени к статическому. [9]
Известна кривая распределения перемещений суппорта по длине направляющих. [10]
Это выражение дает распределение перемещений после окончания удара. [11]
Обычно для определения распределения перемещений и усилий по длине стержня считается удобным использовать метод начальных параметров. Однако как показал проведенный машинный эксперимент, использование этого метода приводит к численным ошибкам. [12]
 |
Примеры полей перемещений. [13] |
Для получения поля распределения перемещения UU ( x, у) вдоль направления х на образец наносится система полос, ориентированных по направлению оси у. [14]
Высказанное предположение о распределении перемещений позволяет определить соответствующие перемещения любой точки тела, которые будут являться линейной функцией координат х и у. Имея выражения для перемещений, нетрудно найти относительные линейные и угловые деформации, а затем определить и напряжения, которые будут являться функцией смещения узловых точек. [15]
Страницы: 1 2 3 4