Распределение - пирсон
Cтраница 1
Распределение Пирсона находит широкое применение в математической статистике и теории надежности. Его используют для оценки согласованности экспериментальных распределений с теоретическими. [1]
Распределения Пирсона включают в себя три главных типа ( I, IV и VI), остальные являются переходными. [2]
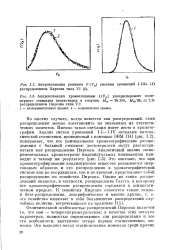
Распределение Пирсона П типа сим метрично и имеет колокол ообразную форму. [3]
Распределения Пирсона полностью определяются первыми четырьмя моментами. [4]
По распределению Пирсона получают вероятности Р ( % 2) достижения критерием х2 данного конкретного значения. При вероятностях, значительно отличающихся от нуля [ расположенных выше главной диагонали в таблице вероятностей /) ( зс2) ], расхождение между эмпирическим и нормальным теоретическим распределением можно считать случайным, а распределение - подчиняющимся закону нормального распределения или другому гипотетическому распределению. [5]
ОС - распределения Пирсона; N, m, 02, ф - усталостные характеристики материала; 5 - интенсивность пульсаций напряжений. [6]
Отличительной особенностью распределений Пирсона является то, что они - четырехпараметрические; в качестве этих четырех параметров, полностью определяющих тип распределения и все его особенности, выступают четыре первых статистических момента. Это выделяет метод статистических моментов среди прочих. [8]
В системе распределений Пирсона плотности (4.2) и (4.3) именуются плотностями типа I и VI соответственна. [9]
Эта функция называется распределением Пирсона или - распределением. [10]
Рг р Хд имеет распределение Пирсона с q степенями свободы. [11]
Такое распределение называется хи-квадрат распределением Пирсона с m степенями свободы. [12]
В теории вероятностей часто рассматривается распределение Пирсона. [13]
Первый случай - III тип распределения Пирсона, b 0 5 - есть распределение Саттарова. [14]
В технических расчетах III тип распределения Пирсона применяется довольно широко. [15]
Страницы: 1 2 3 4