Распределение - погрешность
Cтраница 3
Дифференциальные функции распределения погрешности могут иметь различный вид в зависимости от характера и условий измерений. Обычно на величину погрешности измерения влияет целый ряд обстоятельств и она может быть представлена суммой большого числа составляющих погрешностей, каждая из которых имеет свою причину и свой закон распределения. [31]
Рассмотренная методика распределения погрешностей между отдельными элементами системы и механизма, пользуясь формулами ( 87) - ( 93), проста и дает возможность достаточно быстро производить расчет погрешностей механизмов управления радиоаппаратурой. [32]
Рассмотрим вопрос распределения погрешностей между отдельными элементами данного механизма при проектировании последнего. [33]
Рассмотрим вопрос распределения погрешностей между отдельными элементами в процессе проектирования механизма. [34]
Утверждение, что распределение погрешностей должно обязательно подчиняться нормальному закону, является неверным теоретически и не liujj иер / кдас. Закон нормального распределения получается в тех случаях, когда факторов, вызывающих рассеивание, много, эти факторы взаимно независимы, носят в большинстве случайный характер, не изменяются во времени и среди них нет каких-либо отдельных доминирующих факторов. [35]
Примем, что распределение погрешности хроматографа подчинено закону равномерной плотности. При подобном допущении требования к точности, надежности и динамическим характеристикам хроматографа, рассчитанные по разработанной методике, будут несколько более жесткими. [36]
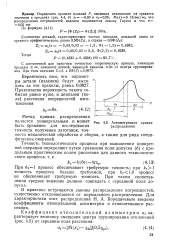 |
Асимметричная распределения. [37] |
Известно, что распределение погрешностей изделия подчиняется закону Гаусса и что а 0 02 мм. [38]
Как известно, распределение погрешности относительного ориентирования Дх близко к закону двухмерного нормального распределения. При независимых х и у сечение поверхности нормального распределения в плоскости хОу образует эллипс, ориентированный главными осями по осям координат. [39]
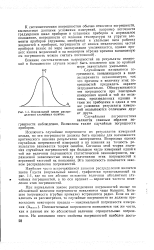 |
Нормальный закон распределения случайных ошибок. [40] |
При нормальном законе распределения погрешностей малые по абсолютной величине погрешности появляются чаще больших. Большие погрешности ( грубые промахи) встречаются редко. Положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные - погрешности. [41]
Методики аппроксимации функций распределения погрешностей, описанные в [33; 51; 52], обладают одной общей особенностью - для их практического применения необходимо знать помимо некоторых качественных признаков реального закона распределения, числовые значения определенных параметров реальных функций распределения. Это ограничивает возможности практического применения этих методик такими областями, где не только доступны оценки соответствующих параметров, но и имеется информация об их стабильности в течение всех процессов измерений, погрешности которых должны быть определены. Реальные условия проведения технических измерений таковы, что на их погрешности влияют и нестабильности свойств применяемых средств измерений и нестабильности окружающих условий и режимов работы объектов измерений. [42]
При произвольном законе распределения погрешности с плавными спадами плотности вероятности эффективное значение погрешности не может быть сразу указано. Однако согласно выражению (1.27) энтропия Н ( х / хц) может быть вычислена для любого закона распределения, а по ней согласно соотношению (1.38) может быть найдено эффективное значение погрешности, которое и предполагается именовать энтропийным значением погрешности. [43]
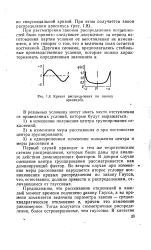 |
Кривая распределения по закону арксинуса. [44] |
При рассмотрении законов распределения погрешностей было принято следующее допущение: за период изготовления партии условия ее и-зготовления не изменяются, а это говорит о том, что и величина поля остается постоянной. [45]
Страницы: 1 2 3 4