Распределение - погрешность - измерение
Cтраница 3
Во всех случаях необходимо оценивать погрешности рассчитываемых характеристик достоверности контроля, обусловленные отличием реального закона распределения погрешности измерений от его принятой аппроксимации. К сожалению, это на практике не делается. Поэтому неизвестно, какую реальную степень доверия заслуживают принимаемые характеристики достоверности контроля, а следовательно, и результаты контроля. [31]
Для выяснения влияния погрешностей измерения на результаты разбраковки контролируемой продукции примем, что априорно известны законы распределения погрешностей измерения. [32]
Особо заметную отрицательную роль играют корреляционные связи между параметрами или погрешностями их измерения, отклонения закона распределения погрешностей измерений от нормального и неисключенные систематические погрешности при обработке больших массивов измерительной информации ( п50) и определении по ней ограниченного числа параметров. Это было замечено при определении параметров движения космических аппаратов по данным большого числа измерений, параметров гравитационного поля Земли по геодезическим и гравиметрическим измерениям. [33]
Значение R определяется раздельно по заданным допускаемым значениям условных вероятностей ложного и необнаруженного отказов с учетом законов распределения погрешностей измерений и значений контролируемого параметра. [34]
В то же время постановка задачи обработки эксперимента, как она сделана Канторовичем, не требует знания информации о статистических свойствах распределения погрешности измерений. Информация о величине предельно допустимой погрешности, как правило, присутствует у экспериментатора, и тогда выполнение условий ( 5) означает, что модель описывает измерения в пределах, обусловленных величиной максимально допустимой погрешности измерений, что совершенно естественно. [35]
Значения параметров разбраковки мало отличаются при распределении погрешности измерения по нормальному закону и закону равной вероятности, принятым за граничные законы распределения погрешностей измерения. [36]
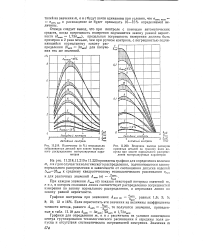 |
Количество ( в % неправильно забракованных деталей при законе нормального распределения контролируемых параметров.| Величина выхода размеров. [37] |
При каждом значении Ажт ( а) показан некоторый интервал значений т, п и с, в котором сплошная линия соответствует распределению погрешностей измерения по закону нормального распределения, а штриховая линия по закону равной вероятности. [38]
При каждом значении ЛмеТ ( т) показан некоторый интервал значений т, п к с, в котором сплошная линия соответствует распределению погрешностей измерения по закону нормального распределения, а штриховая линия по закону равной вероятности. [39]
В дальнейшем графики были рассчитаны Н. Н. Марковым и П. А. Сацердотовым также и для случая, когда распределение отклонений контролируемых размеров следует нормальному закону, а распределение погрешностей измерения - закону равной вероятности. [40]
Для выяснения влияния погрешностей измерения на результаты разбраковки контролируемой продукции примем, что априорно известны законы рассеивания отклонений контролируемых элементов деталей и законы распределения погрешностей измерения. При рассмотрении примем также, что при этом погрешность измерения не имеет систематической составляющей, подчиняется закону нормального распределения и характеризуется практически предельной величиной 8мет и омгп. [41]
Как уже отмечалось, при технических измерениях, а возможно, и при многих лабораторных измерениях, можно считать, что реальные функции плотности распределения погрешностей измерений обычно удовлетворяют трем ограничениям: они усеченные, симметричные, одномодальные. Семейство функций Иордана тоже удовлетворяет этим условиям. [42]
Для этого можно воспользоваться приложением 2 к ГОСТ 8.051 - 81 ( СТ СЭВ 303 - 76), где приведены графики изменения указанных величин в зависимости от закона распределения погрешности измерений и точности технологического процесса из-готовления продукции. [43]
Как следует из рис. 3 - 5, значения параметров разбраковки мало отличаются при распределении погрешности измерения по нормальному закону и закону равной вероятности, принятыми за граничные законы распределения погрешностей измерения. [44]
На основе полученного результата измерения определяется среднее арифметическое значение проведенных измерений х и затем среднее квадратическое отклонение и ( вычисления ведутся, как в примере 1 стр. Распределение погрешностей измерения предполагается здесь следующим закону Гаусса. [45]
Страницы: 1 2 3 4