Распределение - случайная величина
Cтраница 2
Распределение случайной величины F ( fej, 2) называется распределением Фишера с k и k2 степенями свободы. [16]
Какое распределение случайной величины называется равномерным распределением. [17]
Какое распределение случайной величины называется показательным распределением. [18]
Какое распределение случайной величины называется нормальным распределением. [19]
Рассмотрим распределение случайной величины у. [20]
Однако распределения случайных величин не обязательно должны быть одинаковыми. [21]
Если распределение случайной величины т ] зависит только от пробных точек, расположенных в окрестности k - й итерации xk, то говорят о независимом случайном поиске, или поиске без адаптации. Если же на распределение т оказывает влияние предыстория ( ретроспектива) поиска, то говорят о поиске с адаптацией. [22]
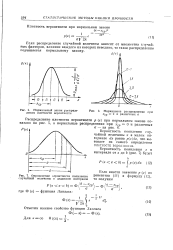 |
Нормальный закон раепреде - [ IMAGE ] Нормальное распределение при.| Определение вероятности появления случайной величины в заданном интервале. [23] |
Если распределение случайной величины зависит от множества случайных факторов, влияние каждого из которых невелико, то такое распределение подчиняется нормальному закону. [24]
Задано распределение случайной величины ( по поводу названий см. стр. [25]
Если распределение случайной величины п известно ( оно определяется выражениями (2.6) и (2.7) ], то легко найти математическое ожидание г /, и дисперсию ( уг - Уг) 2 функции этой случайной величины й ( дс. [26]
Если распределение случайной величины полностью сосредоточено в ограниченной области, то ее моменты всех порядков существуют и полностью определяют ее распределение. [27]
Зная распределение случайной величины, например, зная уравнение кривой распределения, если таковая существует, мы можем вывести все свойства этой величины. Однако во многих случаях ограничиваются более простой задачей, а именно стремятся произвести достаточно надежную оценку соответствующих параметров путем вычисления значений тех или иных статистик. [28]
Если распределение случайной величины, полностью сосредоточено в ограниченной области, то ее моменты всех порядков существуют и полностью определяют ее распределение. [29]
Если распределение случайных величин X - зависит только от одного неизвестного параметра а, то построение доверительного интервала обычно осуществляется с, помощью какой-либо точечной О. [30]
Страницы: 1 2 3 4