Распределение - случайная величина
Cтраница 3
Часто распределение случайной величины X известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются - параметрическими. [31]
Если распределение отдельной случайной величины имеет конечную дисперсию, при суммировании большого числа одинаково распределенных независимых случайных величин предельным будет гауссово распределение. Это означает, что к нормальному распределению притягиваются самые различные распределения с конечными дисперсиями, и объясняет универсальный характер нормального распределения, которое реализуется во многих задачах, когда приходится суммировать большое число независимых случайных величин. Нормальному закону подчинены флуктуации многих наблюдаемых величин, например плотности не слишком сжатого газа. Размытие облака частиц, находившихся в начальный момент в одной точке и совершающих независимое броуновское движение, также описывается нормальным законом. [32]
Тогда распределение случайной величины JJL сходится к распределению Пуассона с параметром А. [33]
Плотность распределения случайной величины полностью определяет случайную величину. [34]
Закон распределения случайной величины, времени жизни элемента т, заданный функцией распределения F ( t), полностью определяет надежность элемента. [35]
Характер распределения случайной величины, графически выражаемой кривой распределения, может быть оценен двумя характеристиками: положением центра группировавания отклонений и средним квадратическим отклонением от этого центра. Значение предельного отклонения определяется в зависимости от значения среднего квадратического отклонения и закона распределения погрешностей. [36]
Характер распределения случайной величины, графически выражаемой в виде кривой распределения, а аналитически - формулой закона распределения р ( х), может быть также оценен его основными численными характеристиками. [37]
Закон распределения случайной величины, Под случайной величиной, связанной с некоторым опытом, понимается всякая величина, которая при осуществлении этого опыта принимает то или иное числовое значение. [38]
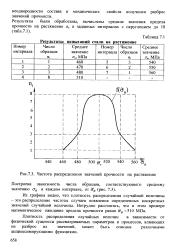 |
Результаты испытаний стали на растяжение. [39] |
Плотность распределения случайных величин в зависимости от физической сущности рассматриваемых параметров и процессов, влияющих на разброс их значений, может быть описана различными аппроксимирующими функциями. [40]
Закон распределения случайной величины, времени жизни элемента г, заданный функцией распределения F ( t), полностью определяет надежность элемента. [41]
Параметры распределения случайных величин - постоянные величины, входящие в закон или функцию распределения. Параметры при неизвестном законе или функции распределения характеризуют, хотя и не так полно как последние, центр рассеяния - математическое ожидание и интенсивность или степень рассеяния - дисперсию. [42]
Асимметрия распределения случайной величины характеризуется третьим центральным моментом, так как если распределение симметрично относительно математического ожидания, то все моменты нечетного порядка равны нулю. [43]
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Для дискретной случайной величины закон распределения часто задается в виде таблицы, в первой строке которой указываются возможные значения случайной величины, а во второй - соответствующие им вероятности. [44]
Законом распределения случайной величины называется любое правило, позволяющее для произвольного набора возможных значений вычислять соответствующие вероятности. [45]
Страницы: 1 2 3 4