Распределение - релей
Cтраница 2
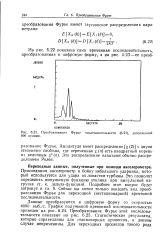 |
Преобразование Фурье последовательности, дополненной 896 нулями. [16] |
Это распределение называют обычно распределением Релея. [17]
УПЧ представляет собой обобщенный закон распределения Релея. [18]
Нормальный закон, экспоненциальный и закон распределения Релея имеют фиксированную форму. Логарифмически нормальный, Вейбулла, гамма-распределения, Стьюдента и другие законы распределения имеют один и более параметров формы, что дает возможность подобрать более точно вид распределения для характеристики полученных экспериментальных данных. Параметр формы можно графически оценить, подбирая значение параметра, которое соответствует наилучшей линейности графика на вероятностной бумаге. Например, требуется определить средний ресурс 60 двигателей СМД-14А по изменению объема прорвавшихся газов в картер. [19]
Такой способ имитации чисел, подчиняющихся распределению Релея, включает в себя вычисление натурального логарифма Обычные стандартные программы предусматривают вычисление In с высокой точностью, как правило, излишней при имитации случайных величин. Поскольку логафримирование является одной из самых медленных операций, реализуемых на ЭВМ, значительно возрастают общие затраты машинного времени имитации случайных чисел, подчиняющихся закону Релея. [20]
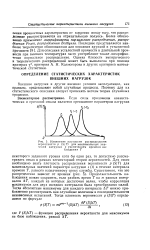 |
Изменение плотности распределения. [21] |
Более обоснованно применение логарифмически нормального распределения, распределения Релея, распределения Вейбулла. Для описания усталостной прочности и длительной прочности при высоких температурах часто употребляют также логарифмически нормальное распределение. Оценка близости эмпирического и теоретического распределений может быть выполнена при помощи критерия уД критерия А. Н. Колмогорова и других критериев математической статистики. [22]
Кроме того, с ним связано так называемое распределение Релея. [23]
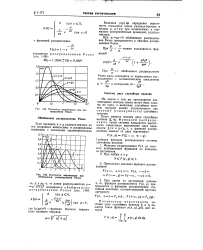 |
Плотность вероятности при распределении Релея.| Плотность вероятности при обобщенной распределении Релея. [24] |
При Ц1 Ц20 обобщенное распределение Релея превращается в обычное распределение Релея. [25]
При т можно видеть, что (2.1.147) приводит к распределению Релея. При значениях и удовлетворяющих условию 0 5 / я1, получаем ФПВ, которая имеет более протяженные хвосты, чем пр распределении Релея. При значениях т хвосты ФПВ распределения Накагами убывают быстрее, чем да распределения Релея. [26]
В классе случайных гауссовских процессов описание замираний огибающей сигнала законом распределения Релея соответствует предельному случаю наиболее глубоких флюктуации. [27]
На рис. 2.7 показан график распределения (2.78), которое известно как распределение Релея, аргументом является безразмерная переменная - нормированная по среднеквадратическому отклонению огибающая А / а ( а - У. [28]
Например, обеспеченность 46 5 % ( т 0 465) по закону распределения Релея соответствует среднему значению амплитуды случайного процесса, что даст A l 25 - ] / Di. Это значение амплитуды было принято в расчетах для ТС. [29]
Предполагается, как уже было упомянуто, что случайные величины Ег подчинены закону распределения Релея, а случайные величины Т - равновероятному закону распределения. [30]
Страницы: 1 2 3 4