Распределение - релей
Cтраница 4
Такими типовыми законами распределения являются распределение Гаусса, или нормальное распределение, равномерное распределение, распределение Пуассона ( для дискретных случайных величин), распределение Релея, Коши и др. Основное распространение в системах автоматического управления имеет нормальное распределение. Практически можно считать, что всякая непрерывная случайная величина, представляющая собой результат действия достаточно большого числа независимых случайных причин, имеет нормальное распределение. [46]
Частный случай W ( a, I, b) известен как двухпарамет-рическое экспоненциальное распределение, a W ( a, 2, b) - как распределение Релея. [47]
Типовыми законами распределения реальных случайных величин являются: распределение Гаусса или нормальное распределение; равномерное и экспоненциальное распределение; распределение Пуассона р ( х) Ххе - х / х; распределение Релея, Коши, Лапласа и др. ( здесь А. [48]
Так, закон Вейбулла ( табл. 10) при ml превращается в экспоненциальный закон, при / л 1 он может быть близок к нормальному, а при m 2 получаем так называемое распределение Релея. [49]
При этом предполагается, что координаты одинаково, распределены по нормальному закону с математическими ожиданиями, равными нулю, и с равными средними квадратическими отклонениями. Распределение Релея определяется одним параметром р, равным среднему квадратиче-скому отклонению исходного двумерного нормального распределения. [50]
Анализируя (6.76), (6.77), (6.85) и (6.86), можно заметить, что для определения помехоустойчивости некогерентного приемника необходимо знать только энергию сигналов и спектральную плотность помехи. Сигнал оставляет свои следы в виде деформации распределения Релея в обобщенное его распределение. [51]
Анализируя (6.76), (6.77), (6.85) и (6.86), можно заметить, что для определения помехоустойчивости некогерентного приемника необходимо знать только энергию сигналов и спектральную плотность помехи. Сигнал оставляет свои следы в виде деформации распределения Релея в обобщенное распределение Релея. [52]
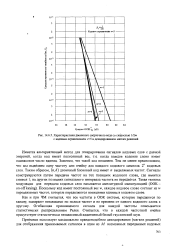 |
Характеристики двоичного сверточного кода со скоростью 112т с кодовым ограничением v5 и декодированием мягких решений. [53] |
Как и при ЧМ считается, что все частоты в ООК системе, которые передаются по каналу, замирают независимо по полосе частот и во времени от одного кодового слова к другому. Огибающая принимаемого сигнала для каждой частоты описывается статистически распределением Релея. Считается, что в каждой частотной ячейке присутствует статистически независимый аддитивный белый гауссовский шум. [54]
В период приработки внезапные отказы описываются распределением Вейбула с параметром т1 или гамма-распределением. В период повышенного износа или старения объекта отказы описываются усеченным нормальным распределением или распределением Релея. [55]
Можно доказать, что сумма достаточно большого числа независимых случайных величин, подчиненных каким угодно законам распределения ( при соблюдении некоторых весьма условных ограничений), приближенно подчиняется нормальному закону распределения. Так, при математическом ожидании т 1 распределение может быть близко к закону Вейбулла, при т - 2 получаем так называемое распределение Релея. [56]
При т можно видеть, что (2.1.147) приводит к распределению Релея. При значениях и удовлетворяющих условию 0 5 / я1, получаем ФПВ, которая имеет более протяженные хвосты, чем пр распределении Релея. При значениях т хвосты ФПВ распределения Накагами убывают быстрее, чем да распределения Релея. [57]
Преимущество закона распределения Вейбулла в том, что он может принимать различный вид вследствие изменения значений параметров. Так, при т 1 закон Вейбулла превращается в экспоненциальный закон, при m 1 он может быть близок к закону нормального распределения, а при т - 2 получают так называемое распределение Релея. [58]
Из различных распределений непрерывных случайных величин, используемых в технике, в данном случае наибольшее значение представляют распределение по закону равной вероятности, нормальное распределение ( распределение по закону Гаусса); нормально-логарифмическое распределение; экспоненциальное распределение, распределение Релея, распределение Эрланга, распределение Вейбулла и гамма-распределение. [59]
Страницы: 1 2 3 4