Распределение - релей
Cтраница 3
 |
Функция [ IMAGE ] Плотность. [31] |
На рис. 3.17 и 3.18 приведены зависимости F ( x) uf ( x) для распределения Релея. [32]
Если замирания сигнала в отдельных ветвях определяются законом Релея, то задача сводится к композиции п распределений Релея. К сожалению, решение этой задачи связано с весьма громоздкими выкладками и его не удается выразить через известные функции. [33]
По своей форме плотность вероятности р ( х h), h 1, приближается к распределению Релея. При h 0 для функций р ( х h нарушается свойство унимодальности: справа от основного максимума ( в области больших х) появляется еще один максимум. [34]
При этом а - 1, а распределение ( 43), очевидно, приближается к распределению Релея. [35]
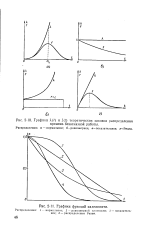 |
Графики A. ( 0 и / ( / теоретических законов распределения времени безотказной работы.| Графики функций надежности. [36] |
Распределения: / - нормальное; 2 - равномерной плотности; 3 - показательное; 4 - распределения Релея. [37]
В литературе по надежности рассматриваются, например, такие законы распределения времени отказов: нормального распределения, распределения Релея, Гамма-распределения, распределения Вейбулла и др. Последнее распределение в известной мере является универсальным, охватывающим несколько других распределений. Например, закон экспоненциального распределения может рассматриваться как частный случай закона распределения Вейбулла. [38]
В настоящей работе рассматривается вопрос, связанный с разработкой ускоренной процедуры имитации случайных чисел, подчиняющихся закону распределения Релея. Необходимость в рационализации приемов моделирования закона Релея возникла в связи с исследованием точности приемочного контроля по двум экстремальным размерам, о чем подробнее будет сказано ниже. [39]
В ряде случаев можно принять, что случайные величины - амплитуды отклонений расположения и формы поверхностей подчинены закону однопараметрического распределения Релея, в котором математические ожидания и дисперсии взаимосвязаны. [40]
 |
Плотность вероятности производной ( tQ в моменты пересечения случайным процессом. ( t заданного уровня. [41] |
К этому классу относятся, ff в частности, стационарные гаус-совские процессы g ( t), процессы с распределением Релея, Раиса, Максвелла, а также процессы с - распределением. [42]
Важно отметить, что на основе формул (4.6.38), (4.6.46) и (4.6.44) подобные результаты могут быть записаны для процессов с распределением Релея, с логарифмически нормальным распределением и для некоторых функционально преобразованных случайных процессов. [43]
 |
Графики плотности распределения Релея и Раиса. [44] |
На рис. 2.7 показаны графики распределения (2.78) ( см. далее (2.86)) при разных ао / Ко, которое при а0 0 известно как распределение Релея, а при ао. [45]
Страницы: 1 2 3 4