Распределение - сегмент
Cтраница 3
Модель, которая лежит в основе уравнения ( 26 - 56) ( раздел 26д), предполагает равномерное распределение неподвижных зарядов внутри сферы с радиусом Re, в то время как усредненное распределение сегментов, даваемое уравнением ( 10 - 26), экспоненциально уменьшается с расстоянием по мере удаления от центра. [31]
Частично несоответствие теории экспериментальным данным может быть связано с введением упрощенных соотношений между такими параметрами, как время релаксации и молекулярная структура полимера, а также с произвольным выбором формы зависимости функции распределения сегментов от скорости сдвига. [32]
Хотя такого результата следовало ожидать для области разбавленных растворов, где ( nVs / RT) 0 - сМ 1, он оказался несколько неожиданным для концентрированных растворов, для которых на основании модели равномерной плотности распределения сегментов по объему я должно было быть функцией только степени объемного заполнения раствора полимером. [33]
В третьем параграфе мы рассматривали статистику отдельной изолированной цепочки, причем считали, что цепь не имеет толщины и собственного объема и, кроме того, в ней отсутствуют какие бы то ни было силы между сегментами. Для распределения сегментов по радиусу клубка приближенно получается гауссова функция, отчего подобные цепи мы будем называть гауссовыми. Перейдем к рассмотрению реальной цепи, каждое звено которой имеет конечный объем. В этом объеме не могут одновременно находиться другие звенья. Поэтому основной эффект конечного объема, являющийся как бы эффектом отталкивания, приводит к большим размерам статистического клубка. Одновременно будем учитывать силы сцепления звеньев друг с другом и с растворителем. [34]
В третьем параграфе мы рассматривали статистику отдельной изолированной цепочки, причем считали, что цепь не имеет толщины и собственного объема и, кроме того, в ней отсутствуют какие бы то ни было силы между сегментами. Для распределения сегментов по радиусу клубка приближенно получается гауссова функция, отчего подобные цепи мы будем называть гауссовыми. Перейдем к рассмотрению реальной цепи, каждое звено которой имеет конечный объем. В этом объеме не могут одновременно находиться другие звенья. Поэтому основной эффект конечного объема, являющийся как бы эффектом отталкивания, приводит к большим размерам статистического клубка. Одновременно будем учитывать силы сцепления звеньев друг с другом и с растворителем. Расчет длины подобной реальной цепи может быть проведен с помощью общих методов статистической механики. [35]
При этом в качестве параметра ориентации используют угол раскрытия конуса. В [1739] предполагают эллиптическое распределение сегментов цепи и рассчитывают дихроичное отношение в зависимости от отношения осей эллипса. [36]
Леннарда - Джонса для низкомолекулярных веществ в основном благодаря наличию экспоненциального члена, описывающего распределение сегментов относительно центра тяжести цепи. Обычно предполагается, что распределение сегментов изолированной макромолекулы относительно ее центра тяжести описывается гауссовой статистикой, однако гораздо более серьезное значение имеет гипотеза относительно того, что потенциал взаимодействия между двумя молекулами может аппроксимироваться суммой потенциалов взаимодействия между сегментами различных молекул. Эта теория описывает наиболее общие свойства полимерных молекул, однако совершенно не учитывает их химическую индивидуальность. Поэтому фундаментальное значение приобретает вопрос о том, что же все-таки следует понимать под взаимодействием между сегментами. Наиболее простое решение состоит в том, чтобы учесть это взаимодействие с помощью соответствующего параметра, как это было сделано в уравнении ( III. В этом случае, естественно, возникает новая проблема - строгое определение понятия сегмента. Однако, как будет показано ниже, в приближенных расчетах это ограничение играет сравнительно малую роль. [37]
В предположении, что сегмент X расположен в любом месте в блоке, Е представляет собой случайную переменную с равномерным законом распределения. Если предположить, что распределение сегментов заданной длины на физическом запоминающем устройстве описывается законом Пуассона и что сегмент-цель ( сегмент Y) есть n - й сегмент за сегментом X, то расстояние D между сегментами X и Y представляет собой случайную величину, описываемую гамма-распределением. [38]
Таким образом, мы получили два фундаментально важных результата. Во-первых, оказывается, что распределение сегментов цепи около начальной точки является гауссовым. Во-вторых, средняя квадратичная длина цепи растет пропорционально корню из числа звеньев. Оба заключения являются обычными для статистически независимых событий. [39]
Учет интерференции и теория флуктуации в принципе эквивалентны. Однако на практике оказывается, что внутримолекулярное распределение сегментов проще рассматривать как интерференционный эффект, тогда как лгежмолекулярное взаи-модействие ( зависящее от концентрации) лучше рас-сматривать на основе флук-туационной теории. [40]
Расстояние между различными поверхностями раздела должно быть несколько большим, чем pfe0 s или qhas из-за частичного перекрывания клубков. Учитывая возможность перекрывания клубков и принимая, что распределение сегментов является гауссовским, оказывается возможным оценить оптимальные расстояния между поверхностями разделов следующим образом. Таким образом, величина 0 55Й0 2 - 0 35А0 I 25h0 может рассматриваться как диаметр агрегата. Кроме того, такое расширение клубка может быть уменьшено из-за необходимости заполнения пространства между поверхностями раздела. Полученные экспериментальные данные ( см. ниже) указывают, что величина I 2h0 является разумной оценкой расстояния между поверхностями раздела. [41]
На основании изучения механизма химической реакции и структуры сшитого полимера, образующегося в концентрированных растворах длинноцепочечных реагентов, Фольмерт предложил модель коллапсированных клубков ( рис. 1.1 г), в соответствии с которой при переходе от разбавленного раствора к концентрированному ( и, в пределе, к блочному состоянию) происходит не перекрывание макромолекулярных клубков, а их сегрегация в изолированные домены; размеры последних изменяются антибатно концентрации раствора. Сходные соображения были положены в основу модели равномерной плотности распределения сегментов в изолированных макромолекулярных доменах. [42]
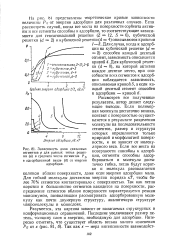 |
Зависимость доли связанных сегментов р для разных типов решетки ( а и среднего числа сегментов РВ в адсорбционной петле ( б от энергии адсорбции. [43] |
Для гибкой молекулы достаточно энергии порядка кТ, чтобы более 70 % сегментов контактировало с поверхностью. Так как петли коротки и большинство сегментов находится на поверхности, распределение сегментов вблизи поверхности характеризуется резким максимумом, позволяющим рассматривать адсорбированную молекулу как почти двумерную структуру, аналогичную структуре макромолекулы в монослоях. [44]
Рассмотрим некоторый элемент объема 8у, в котором присутствуют звенья обоих перепутавшихся клубков. В первом приближении мы считаем, что перепутывание обоих клубков не изменяет распределения сегментов в каждом из них. [45]
Страницы: 1 2 3 4