Распределение - местная скорость
Cтраница 2
Вычисленные рассмотренным здесь методом амплитудная и фазовая частотные характеристики полностью совпадают с теоретическими характеристиками из работы [23], которые также определяли с учетом нестационарности распределения местных скоростей, но более сложным путем. На графиках нанесены заимствованные из упомянутой работы экспериментальные значения относительных амплитуд и фаз. [16]
Изгиб плоской струи теплого воздуха, как известно, определяется главным образом динамическими напорами потоков теплого и холодного воздуха, углом между направлениями движения взаимодействующих потоков и характером распределения местных скоростей в начальном сечении струи. В задачу расчета воздушной завесы входит, главным образом, определение связи между подаваемым расходом теплого воздуха и максимальной высотой подъема теплой струи. Очевидно, задача может считаться решенной, если найдена такая высота Н, при которой проникание холодного воздуха в помещение исключается. [17]
В заключение настоящего параграфа следует отметить, что рассмотренная здесь теория тонкого профиля находит наибольшее применение лишь в задачах, требующих определения суммарных аэродинамических характеристик профиля, так как получаемое с ее помощью распределение местных скоростей ( давлений) по профилю значительно отличается от действительного. [18]
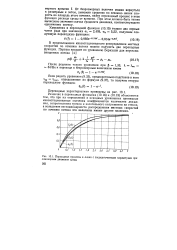 |
Переходные процессы в линии с сосредоточенными параметрами при ламинарном движении среды. [19] |
Различие в переходных функциях (10.18) и (10.19) объясняется тем, что при их определении в исходных уравнениях принимали квазистационарные значения коэффициентов количества движения, сопротивления трения и касательного напряжения на стенке, а вследствие нестационарности распределения местных скоростей по сечению потока эти величины имеют другие значения. [20]
Как видим, значение подъемной силы и момента определяются лишь первыми тремя коэффициентами разложения А0, А и Л2; остальные коэффициенты не влияют на суммарные аэродинамические характеристики ( подъемную силу и момент), а влияют только на распределение местных скоростей по профилю. [21]
Расчеты и эксперименты показывают, что в пристенных слоях жидкости скорости течения изменяются почти синфазно с изменением градиента давления вдоль трубы, в то время как в центральной части потока скорости течения отстают по фазе от градиента давления. Изменение закона распределения местных скоростей по сечению потока при неустановившемся движении среды в трубе сопровождается изменением диссипации энергии. [22]
Комплексное волновое сопротивление ZB ( / со), как показывает соотношение (10.52), с увеличением частоты колебаний со приближается к ZBO, соответствующему волновому сопротивлению без учета вязкости среды, что объясняется возрастающим влиянием на волновое сопротивление инерции среды. Вследствие нестационарности распределения местных скоростей по сечению потока, сопровождающейся повышенной диссипацией механической энергии, сближение этих величин происходит менее интенсивно, чем в предположении квазистационарного сопротивления трения. В последнем легко убедиться, подставив в соотношение (10.52) значения корректива иа, вычисленные при разных со. [23]
Напомним, что неравномерным движением воды называется такое движение, при котором площади живых сечений изменяются по длине потока, или по величине, или по форме. Соответственно изменяются средние скорости и характер распределения местных скоростей. Если изменения происходят достаточно медленно и постепенно, то движение воды называется плавно изменяющимся. В данной главе рассматрлвается именно этот случай, а потому в дальнейшем, говоря о неравномерном движении, будем иметь в виду плавно изменяющееся установившееся неравномерное движение воды в открытом русле. [24]
Из формулы (9.70) видно, что средняя за период колебания мощность NT равна сумме мощности NQ потока, на который накладываются колебания, н мощности, затрачиваемой на поддержание колебаний среды. Если бы мощность NT подсчитывалась в предположении квазистационарного закона распределения местных скоростей, соответствующего течению Пуазейля, то значение х, было бы равно единице и мощность NT имела бы меньшие значения. [25]
Изучение в последние десятилетия турбулентного течения показало, что к стенке русла примыкает заторможенный ею весьма тонкий слой жидкости, называемый пограничным слоем. В этом слое вязкость жидкости оказывает значительное влияние на величину и распределение местных скоростей. [26]
Вычисленные при таком допущении коэффициенты затухания и фазы обозначим соответственно бкс и екс. Отношения 6 / 6кс и е / еко дают представление о том, как влияет нестационарность распределения местных скоростей движения среды на составляющие коэффициента распространения возмущений в линии. [27]
После начала последовательной перекачки позади идущая жидкость Б вклинивается во впереди идущую жидкость Л в соответствии с параболическим профилем распределения местных скоростей. Смесью в данном случае является участок трубы, заполненный сразу обеими контактирующими жидкостями. [28]
После начала последовательной перекачки позади идущая жидкость Б вклинивается в впереди идущую жидкость А в соответствии с параболическим профилем распределения местных скоростей. [29]
После начала последовательной перекачки позади идущая жидкость Б вклинивается во впереди идущую жидкость А в соответствии с параболическим профилем распределения местных скоростей. Смесью в данном случае является участок трубы, заполненный сразу обеими контактирующими жидкостями. [30]
Страницы: 1 2 3