Распределение - местная скорость
Cтраница 3
Для постоянства коэффициента преобразования IJQyi необходимо, чтобы на различных режимах измерения характерное проходное сечение потока сохраняло свою площадь. Однако на режимах течения с невысокими числами Re в реальных вязких потоках наблюдается существенное нарушение этого требования из-за изменений эпюры распределения местных скоростей по поперечному сечению потока, что приводит к изменению закона осреднения скорости по сечению и тем самым сказывается на точности измерения расхода Q. Методы стабилизации указанного явления в принципе одинаковы для всех скоростных преобразователей расходомеров и не зависят от способов получения выходного сигнала уг. Скоростные расходомеры находят широкое применение при исследованиях, их свойства хорошо изучены и подробно описаны в литературе. Поэтому ниже приводится лишь краткая характеристика некоторых расходомеров этой группы для ознакомления читателя с методами стабилизации свойств приемных преобразователей и с эксплуатационными особенностями наиболее часто встречающихся приборов. [31]
Уравнение (9.69) описывает неустановившееся ламинарное движение вязкой несжимаемой среди в трубе при гармонических колебаниях. Несмотря на то, что величины и и ( рг - р2) являются функциями только времени и не зависят от координаты г, благодаря введенным коррективам к, и xpf5 в уравнении учтено изменение распределения местных скоростей по сечению потока, поэтому уравнение (9.69) можно назвать квазиодномерным. [32]
Из гидродинамики известно, что скорость движения жидкости или газа в трубопроводе неодинакова в различных местах сечения потока. Для вполне сформировавшегося установившегося потока местная ( локальная) скорость движения частиц жидкости меняется по сечению от нуля до нуля, проходя через максимум. Распределение местных скоростей по сечению зависит от режима течения. [33]
Из гидродинамики [1-4] известно, что скорость движения жидкости ( газа) в трубопроводе неодинакова в различных местах сечения потока. Для вполне сформировавшегося, так называемого установившегося потока, местная ( локальная) скорость движения частиц жидкости меняется обычно по сечению от нуля до нуля, проходя через максимум. Распределение местных скоростей по сечению в значительной мере зависит от режима течения. При ламинарном режиме течения, представляющем собой упорядоченное послойное движение, отдельные частицы жидкости перемещаются по трубопроводу как бы слоями, не перемешиваясь между собой. [34]
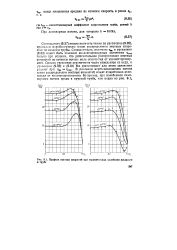 |
Профили местных скоростей при гармоническом колебания жядхоети в трубе. [35] |
Следовательно, величина ъм в уравнении (9.33) может быть заменена квазистационарным значением твкв только при условии, что действительное распределение местных скоростей по сечению потока мало отличается от квазистационарного. Однако указанное ограничение часто упускается из виду, и уравнения (9.33) и (9.34) без достаточного для этого основания решают при тонтокс. В реальном неустановившемся потоке закон распределения местных скоростей может существенно отличаться от квазистационарного. [36]
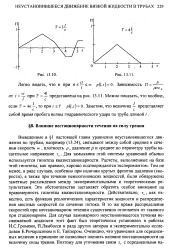 |
Легко видеть, что и при 6 -оо p ( l t O. Зависимость П. [37] |
Выведенные в § 1 настоящей главы уравнения неустановившегося движения по трубам, например (13.24), связывают между собой средние в сечении скорость w, плотность р, давление р и среднее по периметру трубы касательное напряжение тх. Для замыкания этой системы уравнений обычно используется гипотеза квазистационарности. Расчеты, выполненные на базе этой гипотезы, как правило, хорошо подтверждаются экспериментом. Тем не менее, в ряде случаев, особенно при наличии крутых фронтов давления ( скорости), а также при течении неньютоновских жидкостей, были обнаружены заметные расхождения между экспериментальными и теоретическими результатами. Это обстоятельство заставляет обратить особое внимание на правомерность гипотезы квазистационарности. Действительно, хх, как известно, есть функция реологических характеристик жидкости и распределения местных скоростей по сечению потока. В то же время распределение скоростей при нестационарном течении существенно отличается от такового при стационарном. Очевидно, что уравнения для осреднен-ных величин в принципе не позволяют оценить влияние нестационарности на величину силы трения. [38]
Страницы: 1 2 3