Распределение - сумма - независимая случайная величина
Cтраница 1
Распределение суммы независимых случайных величин Xi и X называют композицией распределений этих величин. [1]
Распределение суммы N независимых случайных величин с конечными дисперсиями и с произвольными законами распределения стремится к нормальному распределению при N - оо, если вклад отдельных слагаемых в сумму мал. [2]
Закон распределения суммы независимых случайных величин называется композицией их законов распределения; интеграл в правой части формулы ( 8) называется сверткой функций рх ( х) и ру ( у); таким образом, композиция двух непрерывных законов распределения сводится к свертке их плотностей. [3]
Функция распределения суммы независимых случайных величин, имеющих безгранично-делимые функции распределения, также безгранично-делима. [4]
Функция распределения суммы независимых случайных величин, имеющих безграшпно делимые функции распределения, также & ез-граничяо делима. [5]
Плотность распределения суммы независимых случайных величин называют композицией. [6]
Нахождение закона распределения суммы независимых случайных величин по известным законам распределения слагаемых называется композицией законов распределения. [7]
Определение закона распределения суммы независимых случайных величин zx y по известным законам распределения случайных величин х и у называется композицией законов распределения. [8]
При расчете распределения суммы независимых случайных величин характеристические функции перемножаются. В нашем случае все слагаемые имеют одинаковое распределение. [9]
Нахождение закона распределения суммы независимых случайных величин по известным законам распределения слагаемых называется композицией законов распределения. [10]
Закон Гамма-распределение дает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону. [11]
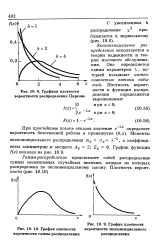 |
Графики плотности вероятности распределения Пирсона.| График плотности вероятности гамма-распределения.| График плотности. [12] |
Гамма-распределение представляет собой распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону. [13]
Характеристические функции позволяют находить распределение сумм независимых случайных величин. [14]
Определение выражения для ряда распределения суммы независимых случайных величин осуществляется с помощью аппарата производящих функций. [15]
Страницы: 1 2 3