Распределение - межатомная функция
Cтраница 3
Нетрудно видеть, что выводы, вытекающие из анализа распределения межатомной функции, почти адекватны тем, которые следуют из анализа статистики отражений ( стр. [31]
Требуется принять во внимание и некоторые сведения, полученные из анализа распределения межатомной функции, и различия атомных весов атомов, и некоторые кристаллохимические и иные соображения, некоторые результаты применения метода проб и ошибок, и сведения, вытекающие из знания дифракционной группы симметрии. На каком-то этапе исследования возникает возможность использовать метод последовательных приближений. На начальной стадии применения метода известны координаты только части атомов элементарной ячейки, и последовательное построение распределения электронной плотности должно выявлять все новые детали структуры. При интерпретации распределений используются общие сведения о строении отдельных групп атомов ( радикалов, комплексов, органических колец, циклов) в сложных молекулах и о примерных межатомных расстояниях. Структурная химическая формула пенициллина в начале исследования не была точно известна. [32]
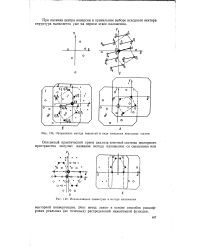 |
Оформление метода смещений в виде смещения векторных систем.| Использование симметрии в методе наложения. [33] |
Этот метод лежит в основе способов расшифровки реальных ( не точечных) распределений межатомной функции. [34]
Однако размывание и объединение максимумов, являющееся следствием конечных их размеров, делает распределение межатомной функции весьма сходным. Только привлечение трехмерного распределения межатомной функции позволило убедительно доказать ложность первоначальных вариантов. Понятно, однако, что аналогичные примеры приблизительной гомометричности возможны и в трехмерном случае. [35]
Из свойств, перечисленных в пунктах г, д, е, следует, что распределение межатомной функции может и не выявить всех деталей системы межатомных векторов. Более слабые максимумы, отвечающие парам легких атомов, тонут в склонах более мощных максимумов, соответствующих тяжелым атомам. Если же все атомы имеют примерно одинаковые атомные номера, система из N ( N-1) максимумов часто оказывается слишком запутанной для быстрого решения задачи. Поэтому метод межатомной функции чаще всего применяется при анализе структур, содержащих относительно небольшое число тяжелых атомов, легко выделяющихся на фоне легких, и используется прежде всего для установления координат именно этих атомов. [36]
Следует, впрочем, отметить, что в данном случае этот изящный по идее метод дает картину, весьма сходную с распределением межатомной функции селената стрихнина. [37]
 |
Графический прием проведения минимализации. [38] |
Прежде чем иллюстрировать изложенное примерами, обратим внимание на удобный графический прием построения минимализованных распределений, применимый в двухмерных случаях. Обычно распределение межатомной функции в проекции ( или в сечении) изображается картой: значения функции фиксируются кривыми равного уровня ( изогипсами), проведенными через одинаковые интервалы величины функции. [39]
Чем выше средняя во времени концентрация электронов вблизи центров атомов, тем резче максимумы распределения электронной плотности и межатомной функции. Разрешающая способность распределения межатомной функции должна несколько повыситься при уничтожении тепловых колебаний атомов. [40]
Существование точного гомометрического дополнения к исследуемой структуре-случай, практически довольно редкий. Однако анализ распределения межатомной функции значительно затрудняется и в тех случаях, когда имеется одна или несколько структур лишь приблизительно гомо-метричных по отношению к исследуемой. [41]
Если оба сорта атомов являются тяжелыми в данной структуре, соответствующие им максимумы будут выделяться в распределении функции Паттерсона своей высотой, что существенно облегчит анализ. На рис. 119 б указано положение максимумов в распределении межатомной функции. [42]
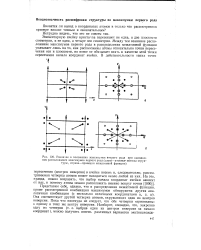 |
Различие в положении максимумов второго рода при одинаковом расположении максимумов первого рода ( слева-атомные мотивы структуры, справа-проекции межатомной функции. [43] |
Элементарную ячейку кристалла пересекают не одна, а две плоскости симметрии, и не одна, а четыре оси симметрии. Между тем взаимное расположение максимумов первого рода в распределении межатомной функции указывает лишь на то, как расположены атомы относительно точки пересечения оси и плоскости, но вовсе не обязывает взять в качестве этой точки пересечения начало координат ячейки. [44]
Отсутствие тяжелых атомов значительно осложняет проблему анализа распределения функции Паттерсона. Если все атомы близки по своей рассеивающей способности, распределение межатомной функции будет содержать большое количество мало отличающихся по высоте максимумов, идентификация которых далеко не всегда возможна. Искажения в положениях и высотах максимумов, вызванные наложениями их друг на друга, создают дополнительные трудности. [45]
Страницы: 1 2 3 4