Распределение - время - ожидание
Cтраница 1
Распределение времени ожидания для единиц различных классов описывается довольно-таки сложными функциями ( см. работу [8]), но среднее время ожидания и среднее число единиц различных классов в системе определяются достаточно просто. [1]
СМО распределение времени ожидания характеризуется соответствующей сверткой распределения обслуживания. [2]
Функция распределения времени ожидания появления двойников, построенная на вероятностной бумаге Гнеденко - Вейбулла. [3]
Функция распределения времени ожидания конца обслуживания вызова каждым коммутатором складывается из времени ожидания начала обслуживания и времени самого обслуживания. Вероятностное распределение этого времени отображается однофазной однолинейной СМО вида М / М / 1 / оо, а изображения их плотностей следуют из результатов гл. [4]
Моменты распределения времени ожидания начала обслуживания заявки некоторого потока в системе с зонами прерываний равны соответствующим моментам в системе с относительными приоритетами, в которой длительности обслуживания различных заявок равны временам пребывания в зонах недоступности для заявок этого потока. [5]
 |
Диаграмма прохождения очередей в системе с быстрой коммутацией. [6] |
Определим функцию распределения времени ожидания ( ФРВО) конца обслуживания вызова в системе с быстрой коммутацией каналов на основании диаграммы прохождения очередей. [7]
Согласно этим уравнениям, функция распределения времени ожидания определяется как решение интегрального уравнения, похожего на известное уравнение Винера - Хопфа. Получим такие же соотношения для характеристик времени незанятости прибора. [8]
Проведен теоретический анализ вида функции распределения времени ожидания первого центра кристаллизации при гомогенной и гетерогенной нуклеации в переохлажденных расплавах и пересыщенных растворах. Показано, что для гомогенной нуклеации Функция распределения при постоянном пересыщении подчиняется либо экспоненциальному закону, либо асимптотическому распределению Вейбулла - Гнеденко. Статистика начальной стадии образования центров кристаллизации в расплавах и растворах, содержащих гетерогенности, в общем случае описывается суперпозицией указанных соотношений. [9]
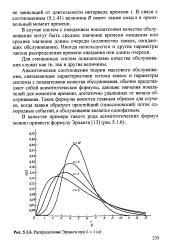 |
Распределение Эрланга при А. 1 ( а. [10] |
Иногда используются и другие параметры закона распределения времени ожидания или длины очереди. [11]
В условиях задачи 10.4 найти закон распределения времени ожидания очередного автобуса, если поток автобусов представляет собой поток Эрланга k - ro порядка. [12]
Эти вероятности определяются в случае, если известны законы распределения времени ожидания для различных типов заявок. Это обстоятельство ограничивает возможность применения указанного критерия. [13]
Как видим, при использовании метода многих проб функция распределения времени ожидания появления первого центра кристаллизации будет соответствовать эмпирической функции распределения для каждого отдельного образца, измеренной по методу одной пробы. Вид этих функций распределения, а также величины соответствующих дисперсий позволяют сделать некоторые выводы о концентрации гетерогенностей и их распределении по активности. [14]
Поставим перед собой задачу - найти вероятности различных состояний системы и функцию распределения времени ожидания в рамках изложенной модели явлений. [15]
Страницы: 1 2 3