Распределение - время - ожидание
Cтраница 2
В двух предшествующих главах мы, следуя классическим работам Эрланга, нашли закон распределения времени ожидания в двух наиболее простых предположениях относительно закона распределения длин разговоров: в случае показательного распределения ( см. гл. [16]
Для расчета среднего времени выигрыша при мгновенном обнаружении неисправностей и реальной системе обслуживания необходимо описание распределения времени ожидания начала обслуживания для конкретных характеристик системы обслуживания. [17]
В применении к теории очередей (5.9) означает, что если время обслуживания распределено показательно, то распределение времен ожидания стремится к показательному пределу. [18]
Функцию распределения TV ( re) ( индексы условно опущены) можно получить при известной функции распределения времени ожидания W ( t) на основе следующего. [19]
Кроме этих данных, модель также позволяет получить 1) распределение времени оборота запросов; 2) распределение времени ожидания в очередях; 3) максимальные длины очередей; 4) средние длины очередей; 5) общее количество запросов, прошедших все очереди с нулевым временем ожидания. [20]
Обозначим w - время ожидания обслуживания в стационарном режиме и и ( х) - стационарную плотность распределения времени ожидания и. [21]
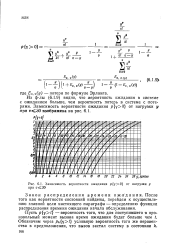 |
Зависимость вероятности ожидания р у0 от нагрузки у при 1 30. [22] |
После того как вероятности состояний найдены, перейдем к осуществлению главной цели настоящего параграфа - определению функции распределения времени ожидания начала обслуживания. [23]
Эта программа позволяет с заранее заданной точностью 8 для определенного значения аргумента t Т вычислить значение функции распределения времени ожидания начала обслуживания. [24]
При необходимости выполнения оценок вероятности задержки информации в памяти ЦВМ при пуассоновских входных потоках заявок может быть использована такая же аппроксимация распределения времени ожидания заявок в очереди, которая использовалась для одномерного потока заявок (3.1.27), но при этом значение W определяется из выражения (3.1.32) или же измеряется экспериментально. [25]
Так как функция f ( f) просто выражается через функцию g ( t), то этим мы получим явное выражение для закона распределения времени ожидания. [26]
В существующей монографической литературе по теории массового обслуживания книга А. Я. Хинчина занимает значительное место, поскольку в ней впервые - было систематически изучено строение входящего потока требований, а также распределение времени ожидания для системы с очередью при обслуживании ее одним прибором. Заметим, что именно в этой монографии А. Я. Хинчин изложил свои достаточные условия близости суммарного потока, слагаемые которого независимы и равномерно малы, к простейшему потоку. По сути дела, как это выяснил ученик А. Я. Хинчина Г. А. Ососков, условия Хинчина являются и необходимыми. [27]
После того, как функции WH ( P) - найдены, по ф-ле (6.2.24) можно определить и преобразование Лапласа функции f ( t), а значит, и саму функцию распределения времени ожидания. Таким образам, соотношения (6.2.23), (6.2.24) и (6.2.25) решают поставленную задачу определения функции распределения времени ожидания. [28]
Площадь ( / от - / ()) о - / стТн в данном случае разбивается на две области, имеющие противоположные знаки ( см. рис. 20 6) Таким образом, статистические исследования кинетики нуклеации позволяют определить из эмпирической функции распределения времени ожидания появления первого центра кристаллизации все характеристики нестационарного периода нуклеации, рассматриваемые классической теорией: временную зависимость скорости нуклеации и период нестационарности. [29]
Однако эти вычисления оказываются весьма трудоемкими, особенно при большом количестве градаций приоритета. Еще более сложными оказываются аналитические выражения для функции распределения времени ожидания заявок в очереди. Эти выражения настолько громоздки, что в явном виде в литературе обычно не приводятся. Влияние вида функций распределения времени обслуживания заявок Bh ( t) на величину среднего времени ожидания заявок в очереди Wk оказывается таким же, как и для рассмотренного ранее случая приоритетного обслуживания по одной заявке от каждого потока заявок. [30]
Страницы: 1 2 3