Распределение - время - релаксация
Cтраница 2
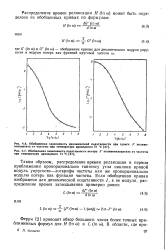
Чтобы найти распределение времен релаксации Хино [185] чиз-мерял ток деполяризации после выдержки образца под напряжением в течение 20 с при разных температурах через каждые - 10 С. Он полагал, что за такой короткий промежуток времени ориентируются диполи приблизительно с одним временем релаксации. В результате была получена зависимость энергии активации от температуры. [16]
Для определения распределения времен релаксации Хино [274] измерял ток деполяризации после выдержки образца под напряжением в течение 20 с при разных температурах через каждые - 10 С. Он полагал, что за такой короткий промежуток времени ориентируются диполи приблизительно с одним временем релаксации. В результате была получена зависимость энергии активации от температуры. [17]
При сужении распределения времен релаксации вид зависимости i ( T) должен обращаться в зависимость вида ( 205), полученную строгим путем, или близкую зависимость. [18]
В реологии распределения времени релаксации для такого случая иногда называют клиновым видом распределения. [19]
Для расчета распределения времен релаксации или запаздывания исходные экспериментальные данные должны охватывать период времени в 10 - 15 десятичных порядков. Получить такие данные для одной температуры чрезвычайно трудно. [20]
В реологии распределения времени релаксации для такого случая иногда называют клиновым видом распределения. [21]
 |
Релаксационный спектр и стрелка действия. [22] |
Определим функцию распределения времен релаксации структуры q ( т), которую для общности будем считать непрерывной. [23]
Таким образом, распределение времен релаксации в первом приближении пропорционально тангенсу угла наклона кривой модуль упругости-логарифм частоты или же пропорционально модулю потерь как функции частоты. [25]
На кривых функции распределения времен релаксации при температуре 70 наблюдается максимум, обусловленный распадом полисульфидных связей. [26]
Обычно форма функции распределения времен релаксации rf ограничивается использованием фигур типа прямоугольника ил и клина. [27]
Я) называют распределением времен релаксации, хотя на самом деле она представляет собой распределение модулей. Не следует думать, что интегральная форма Er ( t) всегда эквивалентна обобщенной модели Максвелла. Формула (3.98) - математическая модель релаксации напряжения и связана с выражением (3.96) только по форме и по заложенным в нее принципам. [28]
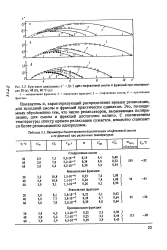 |
Параметры диэлектрической релаксации глифталевой смолы и ее фракций при различных температурах. [29] |
Показатель а, характеризующий распределение времен релаксации, для исходной смолы и фракций практически одинаков. Это, по-видимому обусловлено тем, что число релаксаторов, вызывающих поляризацию, для смолы и фракций достаточно велико. С увеличением температуры спектр времен релаксации сужается, вещество становится более релаксационно однородным. [30]
Страницы: 1 2 3 4 5