Распределение - шум
Cтраница 1
Распределение шума на входе нормальное. [1]
Функция распределения шума имеет Гауссовы характеристики. Функциональная зависимость среднеквадратичной величины шума от площади зрачка, независимо от того, управляется ли эта площадь светом или аккомодацией, обусловливает мультипликативную модель шума. [2]
При частотной модуляции распределение основных составляющих шумов по групповому спектру весьма неравномерно. [3]
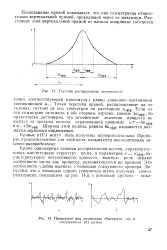 |
Гауссово распределение вероятности. [4] |
Кроме одномерных законов распределения шумов, характеризующих амплитудную структуру шума, и параметров и, иэфф, характеризующих интенсивность процесса, важную роль играют особенности шума как процесса, развивающегося во времени. Эти особенности удобно выявить с помощью следующего примера. [5]
Дополнительно предполагается, что распределение шума w - нормальное. Гауссовость сигнала у не предполагается. [6]
В случае известной плотности w распределения шума АОИ-алгоритмы обеспечивают потенциальную помехоустойчивость обнаружения и различения сигналов. Однако их характеристики весьма чувствительны к отклонению ПРВ шума от плотности w, принятой при синтезе алгоритма. [7]
Эти расчеты показали, что для каждого распределения шума существует оптимальное значение допт параметра д, при котором величина Аад ( q) достигает максимума. [8]
Модель We применяется в том случае, когда ожидаемые распределения шума близки к некоторому известному распределению. В случае значительной априорной неопределенности распределений шума используются модели W5 и W057, которые при необходимости могут быть существенно расширены за счет введения априорно неопределенного параметра масштаба. [9]
Обращаясь к теореме Бейеса (5.149), можно видеть, что распределение шума п часто известно. Следовательно, известна также и плотность вероятности р ( z p), но априорная плотность вероятности р ( ji) часто неизвестна и поэтому предполагается равномерной. [10]
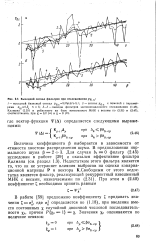 |
Выходной сигнал фильтров при отслеживании yg c. [11] |
Величина коэффициента ( 3 выбирается в зависимости от тяжести хвостов распределения шума. [12]
На основе АРИ-алгоритма, соответствующего расширенной q - то-чечной модели распределений шума, разработан адаптивный вариант этого алгоритма. В качестве варьируемого параметра алгоритма выбран параметр д, который подстраивается по обучающей выборке под фактическое распределения шума путем максимизации специальной целевой функции. [13]
Из этих основных определений получены параметры, отражающие свойства одновременной плотности распределения шума. [14]
При низкой плотности записи преобладающую роль играет структурный шум и закон распределения шумов мало отличается от нормального. [15]
Страницы: 1 2 3 4