Обобщенное распределение

Cтраница 1

Обобщенное распределение при такой схеме суммирования является совокупностью отдельных настроечных партий, которые последовательно связаны с отдельными участками кривой износа. [1]

Обобщенное распределение Эрланга применяется при создании как чисто математических, так и имитационных моделей в двух случаях. [2]

Тема обобщенных распределений в фазовом пространстве и ассоциированного упорядочения операторов была раскрыта в работе Вигнера ( Wigner, 1932), которая упоминалась в разд. Мойал ( Moyal, 1949) развил эту концепцию еще дальше и показал, что распределение Вигнера соответствует вычислению средних значений операторов в симметричном или вейлевском порядке. Нижеприведенный анализ основан, главным образом, на работе Агарвала и Вольфа ( для обзора см. также Perina, 1985, гл. [3]

Из графика обобщенного распределения следует, что 50 - - 90 % всех встречающихся процессов в машинах и механизмах имеют ширину спектра в пределах 150 - - 6 - Ю3 Гц. Наибольшее значение ширины спектра имеют ударные процессы. [4]

Замечательное свойство обобщенного распределения Пуассона является поводом для некоторых любопытных умозаключений. [5]

Для чего используется обобщенное распределение Эрланга. [6]

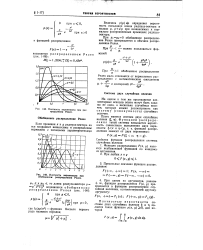Плотность вероятности при распределении Релея.| Плотность вероятности при обобщенной распределении Релея. [7]

При Ц1 Ц20 обобщенное распределение Релея превращается в обычное распределение Релея. [8]

Уравнение (10.36) выражает обобщенное распределение вероятностей времени безотказной работы. [9]

Еще один вариант обобщенного распределения Пуассона будет приведен в примере гл. [10]

По форме распределение (2.1.20) напоминает обобщенное распределение Гиббса (1.3.127), которое использовалось для описания состояния с фиксированными полумакроскопическими флуктуациями. Следует, однако, иметь в виду, что лагранжевы множители в этих двух распределениях определяются из совершенно разных дополнительных условий. [11]

Распределение (4.7) часто также называют обобщенным распределением Релея. [12]

Для проверки правильности принятой гипотезы ( обобщенное распределение является композицией нормального закона и закона равной вероятности) и определения практических значений коэффициентов относительной асимметрии а и относительного рассеивания К были проведены экспериментальные исследования точности обработки отдельных настроечных партий с последующей математической обработкой полученных практических данных. [13]

Наибольшего внимания заслуживает частный случай - обобщенное распределение Пуассона. [14]

Среднее значение ( математическое ожидание) обобщенного распределения погрешностей в любой момент времени равно функции a ( t), рассчитываемой по вышеприведенной формуле. [15]

Страницы: 1 2 3 4