Обобщенное распределение
Cтраница 3
Результаты предыдущего раздела можно теперь переформулировать следующим образом: если существует процесс, удовлетворяющий условиям а) и б), то его Приращения Z ( / A) - Z ( /) имеют обобщенные распределения Пуассона. [31]
Необходимо подчеркнуть один чрезвычайно важный момент, связанный с масштабами осреднения. Модельные обобщенные распределения характеристик задаются обычно непрерывными функциями геометрических координат. Поэтому в рамках каждой модели значение характеристики - проницаемости, теплопроводности, выделения или поглощения массы ( или тепла) - может быть определено для каждой геометрической точки. Но эта непрерывность функции необходима лишь для выполнения математических операций. [32]
Следует иметь в виду, что это утверждение верно только для целочисленных случайных величин. Понятие обобщенного распределения Пуассона остается осмысленным даже тогда, когда X; имеют произвольное распределение, а аналог соотношения (2.3) играет важную роль в общей теории случайных процессов с независимыми приращениями. Однако распределения таких процессов могут и не быть обобщенными распределениями Пуассона. [33]
Дополнения сделаны главным образом в III, IV, V и VII главах. III глава дополнена изложением обобщенного распределения Гиббса и более полным изложением большого канонического ансамбля. В IV главе дополнительно рассмотрены флуктуации давления при фиксированном объеме и дано краткое изложение теории уравнения Колмогорова. В V главе несколько подробнее дана цепочка уравнений Боголюбова. [34]
Ниже будет представлено обобщенное представление оператора плотности, первоначально введенное Кохеном, и примененное к квантовой оптике Агарвалом и Вольфом. Q - и И - распределения получаются из обобщенного распределения как частные случаи. [35]
Анализируя (6.76), (6.77), (6.85) и (6.86), можно заметить, что для определения помехоустойчивости некогерентного приемника необходимо знать только энергию сигналов и спектральную плотность помехи. Сигнал оставляет свои следы в виде деформации распределения Релея в обобщенное распределение Релея. [36]
Разумеется, теперь перед нами встает обратная задача: каждому ли семейству обобщенных распределений Пуассона соответствует некоторый случайный процесс. Ответ на этот вопрос утвердительный, однако ( несколько неожиданно) оказывается, что двух наших условий не достаточно для однозначного определения процесса. [37]
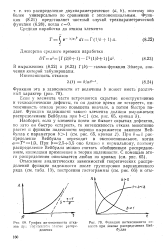 |
График интенсивности отказов пр.. горуалпюм гахоне распределения.| Функция интенсивности отказов при законе распределения Вей. [38] |
При 6 1 распределение Вейбулла переходит в экспоненциальное, когда а - Т - 1 / К. При 6 - 2 5 - 3 5 оно близко к нормальному, поэтому распределение Вейбулла можно считать обобщенным распределением, нашедшим применение в теории надежности. [39]
Сеть процессов, образующих учебный план, - довольно сложная, полнодоступная. Поэтому в практических расчетах будем считать, что поток групп - пуассоновский, а размер группы распределен по закону обобщенного распределения Эрланга. [40]
Джонсон и Клинкенберг [11, 13] подтвердили, что распределения длин цепей в интервале температур ( - 67) - ( - 25) С получаются с помощью одного и того же обобщенного распределения, которое в различной степени искажено в своей правой части. При более высоких температурах ( - 4) - ( 17) С получаются расхождения между предполагаемыми распределениями и обобщенным распределением. [41]
Отбросим из рассмотрения группы Gi и GJ, заменив их группой GJJ, и повторим описанный в последних двух абзацах процесс. После k - 1 повторений станут известны относительные сдвиги для всех k алфавитов. Кроме того, будет найдено обобщенное распределение частот. Для того чтобы найти исходные эквиваленты букв шифрованного текста, переупорядочим последние согласно их частотам. Теперь нетрудно восстановить весь квадрат Виженера и расшифровать текст. Ключевое слово можно найти, перебрав 32 набора из k букв, относительные расстояния между которыми соответствуют найденным сдвигам алфавитов. Возможно, что некоторые редко встречающиеся буквы окажутся не на своих местах. [42]
Следует иметь в виду, что это утверждение верно только для целочисленных случайных величин. Понятие обобщенного распределения Пуассона остается осмысленным даже тогда, когда X; имеют произвольное распределение, а аналог соотношения (2.3) играет важную роль в общей теории случайных процессов с независимыми приращениями. Однако распределения таких процессов могут и не быть обобщенными распределениями Пуассона. [43]
Во-вторых, в реальной жизни существует объективная вероятность возникновения групп заявок в качестве реакции на какие-то действия, поэтому возникают групповые потоки. Применение чисто математических методов для исследования в моделях эффектов от таких групповых потоков либо невозможно из-за отсутствия способа получения аналитического выражения, либо затруднено, так как аналитические выражения содержат большую систематическую погрешность из-за многочисленных допущений, благодаря которым исследователь смог получить эти выражения. Для описания одной из разновидностей группового потока можно применить обобщенное распределение Эрланга, которое рассмотрим ниже. Внешне похожее на гамма-распределение, оно имеет свои математические особенности. [44]
Джонсон и Клинкенберг [11, 13] подтвердили, что распределения длин цепей в интервале температур ( - 67) - ( - 25) С получаются с помощью одного и того же обобщенного распределения, которое в различной степени искажено в своей правой части. При более высоких температурах ( - 4) - ( 17) С получаются расхождения между предполагаемыми распределениями и обобщенным распределением. [45]
Страницы: 1 2 3 4