Логнормальное распределение

Cтраница 1

Логнормальное распределение широко применяется в самых различных областях естествознания. Большой объем работ был также проделан геологами по проверке согласия с логнормальным законом выборочных распределений содержаний редких и малых элементов в породах различного генезиса. Хотя во многих случаях аппроксимация логнормальным распределением вполне удовлетворительна, надлежащее теоретическое обоснование, ведущее именно к логнормаль-ной модели, почти всегда отсутствует. Это не позволяет исследователю дать генетическую интерпретацию полученных таким путем вероятностных моделей. [1]

Логнормальное распределение можно использовать в качестве первого приближения для описания относительного изменения цен активов, однако, с теми ограничениями, о которых было сказано при обсуждении распределения Гаусса. [2]

Кроме того, логнормальное распределение является привлекательным с точки зрения применения его по отношению к ценам активов, так как диапазон этого распределения находится в интервале от 0 до оо. Этот диапазон в точности схож с теоретическим диапазоном цен активов потому, что они не могут быть отрицательными, но могут принимать очень высокие положительные значения. [3]

Рассмотрим теперь класс логнормальных распределений. [4]

Распределение для а хорошо моделируется логнормальным распределением, т.е. - log a аппроксимируется гауссовским распределением. Параметр задержки, по данным измерений, равен т0 6 3 не. [5]

Расчет кривых модифицированных фазовых проницаемостей для логнормального распределения проницаемости Талинскои площади при среднеквадратичном ее отклонении 0; 0 5; 1 0; 1 5 приведен в разд. [6]

Непрерывная случайная величина X имеет логарифмически-нормальное ( сокращенно логнормальное распределение), если ее логарифм подчинен нормальному закону. [7]

Пусть выборка размером п 1 8 из логнормального распределения находится в переменной EX. [8]

Зависимость безразмерной эффективной проводимости и / з0 от коэффициента вариации проводимости. [9]

Нелишне отметить, что в предположении о логнормальном распределении проницаемости а формула (6.132) является точной. [10]

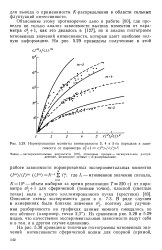Нормированные моменты интенсивности 3, 4 и 5-го порядков в зависимости от параметра а / 1 / 2 / / 2. [11]

Точки - экспериментальные результаты [127], сплошные кривые - логнормальное распределение, штриховые кривые - / ( - распределение. [12]

Непрерывная случайная величина X имеет логарифмически нормальное ( сокращенно - логнормальное распределение), если ее логарифм подчинен нормальному закону. [13]

Кроме нормального, пуассоновского и гамма-распределений, безгранично делимо и логнормальное распределение. Логнормальным называется распределение положительной случайной величины, логарифм которой нормально распределен, см. статью Торина. Безгранично делимы также t - распределение Стьюдента и распределение Коши ( распределение отношения двух независимых случайных величин, имеющих стандартное нормальное распределение), см. книгу Лукача и статьи Гроссвальда, Эп-штейна и Бондессона. [14]

Кроме нормального, пуассоновского и гамма-распределений, безгранично делимо и логнормальное распределение. Безгранично делимы также / - распределение Стьюдента и распределение Коши ( распределение отношения двух независимых случайных величин, имеющих стандартное нормальное распределение), см. книгу Лукача и статьи Грос-свальда, Эпштейна и Бондессона. [15]

Страницы: 1 2 3 4