Островершинное распределение

Cтраница 1

Островершинные распределения характеризуются более выраженным, чем у нормального распределения, пиком и полого спадающими, тяжелыми хвостами. [1]

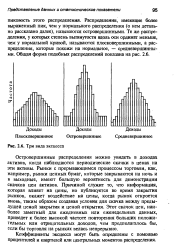Три вида эксцесса. [2]

Островершинные распределения можно увидеть в доходах активов, когда наблюдаются периодические скачки в ценах на эти активы. Рынки с прерывающимся процессом торговли, как, например, рынки ценных бумаг, которые закрываются на ночь и в выходные, имеют большую вероятность для демонстрации скачков цен активов. Причиной служит то, что информация, которая влияет на цены, но публикуется во время закрытия рынков, окажет воздействие на цены, когда рынок откроется вновь, таким образом создавая условия для скачка между предыдущей ценой закрытия и ценой открытия. Этот скачок цен, наиболее заметный для ежедневных или еженедельных данных, приведет к более высокой частоте повторения больших положительных или отрицательных доходов, чем предполагалось бы, если бы торговля на рынках велась непрерывно. [3]

Это толстохвостое, островершинное распределение является характерной формой распределения Парето. [4]

Так, при островершинном распределении центральный столбец шириной d при построении полигона полезно рассматривать состоящим из двух столбцов шириной d / 2, а самые крайние столбцы, вопреки рекомендации В. [5]

Оценка в виде медианы эффективна только для островершинных распределений, Щ я шюсковершинных и двухмодальных распределений эффективность, медианы падает вплоть до нуля. При островершинных распределениях ( рис. 4 - 3, а) экспериментальные точки в центре распределения располагаются плотно и медиана опре - деляется более точно. При плосковершинных ( рис. 4 - 3 6), а тем более при двухмодальных распределениях ( рис. 4 - 3, в) экспериментальные точки в центре располагаются редко и неопределенность медианы резко возрастает, что показано кривыми Хмг на рис. 4 - 2, а для композиций экспоненциальных и двузначного дискретного распределений: При симметричных двухмодальных распределениях ( рис. 4 - 3, в) экспериментальные точки группируются наиболее плотно в области 25 % - и 75 % - ной квантилей, которые Дж. [6]

Оценка в виде медианы эффективна только для островершинных распределений. Для плосковершинных и двухмодальных распределений эффективность медианы падает вплоть до нуля. Это иллюстрируется рис. 4 - 3, где одновременно с формой распределений засечками схематически показано расположение экспериментальных точек на оси к. При островершинных распределениях ( рис. 4 - 3, а) экспериментальные точки в центре распределения располагаются плотно и медиана определяется более точно. При плосковершинных ( рис. 4 - 3 6), а тем более при двухмодальных распределениях ( рис. 4 - 3, в) экспериментальные точки в центре располагаются редко и неопределенность медианы резко возрастает, что показано кривыми ХИ2 на рис. 4 - 2, а для композиций экспоненциальных и двузначного дискретного распределений. При симметричных двухмодальных распределениях ( рис. 4 - 3, в) экспериментальные точки группируются наиболее плотно в области 25 % - и 75 % - ной квантилей, которые Дж. [7]

Стьюдента ( включая распределение Коши), экспоненциальные, двухмодальные кругло-и островершинные распределения, выделив отдельно класс арксинусои-дальных распределений. [8]

Стьюдеита ( включая распределение Коши), экспоиеициальные, двухмодальиые кругло-и островершинные распределения, выделив отдельно класс арксинусои-дальных распределений. [9]

Проведенные вместе параллельные определения не всегда можно считать нормально распределенными величинами. Они приводят к островершинному распределению частот ( рис. 2.6, а) и дают заниженную ошибку метода. [11]

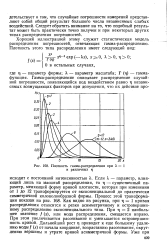Плотность гамма-распределения при К 1 и различных т ]. [12]

Если Я - параметр, влияющий лишь на масштаб распределения, то TJ - существенный параметр, меняющий форму кривой плотности, которая при изменении от 1 до 12 трансформируется от экспоненциальной до практически симметричной колоколообразной формы. Как видно из рисунка, при г 1 кривая распределения относится к резко асимметричному и островершинному распределению экспоненциального типа. При т) 2 наибольшее значение / ( х), или мода распределения, смещается вправо. При этом увеличивается рассеивание и уменьшается островершинность кривой. Дальнейший рост ц приводит к еще большему удалению моды / ( х) от начала координат, возрастанию рассеивания, округлению вершины и утрате кривой асимметричной формы. [13]

Интуитивно понятно, что коэффициент цензурирования должен зависеть от объема выборки и рассчитанного по выборке значения эксцесса. Действительно, такое отклонение от центра, которое является промахом для средневершинного ( а тем более плосковершинного) распределения, для островершинного распределения с его длинными тяжелыми спадами может безусловно принадлежать выборке. [14]

Количество интервалов группировки должно быть нечетным числом. При четном числе столбцов область вблизи центра распределения будет описываться двумя симметрично расположенными относительно центра столбцами гистограммы, тем самым пик распределения будет неоправданно сглаживаться. Это особенно критично для островершинных распределений. Как уже говорилось выше, три столбца дают очень мало информации о форме распределения. Поэтому будем считать, что количество столбцов гистограммы должно быть нечетным числом не менее пяти. [15]

Страницы: 1 2